FOREWORD
Before I post the next part, I want to point out I had to spend a few hours debugging the auto-evo script because of the additions from this part. I finally figured out it was because of inconsistencies in the units. Some measurements were per month (like mating frequency), some were per second (like speed), and some were per individual while others were per the entire species. So I went through all the code and converted everything into SI units (the standard for science), and managed to finally fix it. It doesn’t really apply to you as the reader too much, but you might notice small inconsistencies with the numbers in Parts 1 and 2 with the future parts, and that’s because of this conversion. Anyways, on to the part!
Part 3: Movement
So far, the species has been hunting instantaneously, and therefore spending all of its actual time reproducing. Thus it was only limited in its growth by how often it could reproduce based on physical limits. Now let’s take the first step to fixing that and introduce some time dependence on hunting. This is the first step towards differentiating between the different life activities of the species and time spent between them.
From our current list of assumptions, here is the assumption we will address this part:
- Modelus Specius is a flat, tiny, simple, jelly-like organism that lives at the bottom of the ocean.
- Members of the species can instantly perceive food regardless of distance (Perception)
- Members of the species can instantly teleport to perceived food (Movement)
- Which we will remove and replace by actually tracking the time taken to reach food.
- Members of the species can completely consume the food and gain 100% of the energy. (Hunting/Metabolism)
- The species is equally distributed/dispersed across the world (Demographics)
- The planet is one giant ocean of equal pressure water that is equally accessible to the player (Geography/Terrain)
- Modelus Specius is the only species on the planet (Ecology)
- Members can reproduce as many times as they want, instantly, with no pregnancy/gestation period. (Reproduction)
- The species reproduces via asexual reproduction, spawning fully developed offspring that can themselves immediately begin reproducing. (Mating)
- The species does not change in physiology as they age (Aging/Ontogeny)
- The species is fully aquatic (Terrestriality)
- Members of the species are solitary and do not cooperate with other species members in any way. (Cooperation/Sociality)
- The species has no parental instincts, and will immediately abandon offspring (Parenting)
- The species is perfectly adapted to its environment and suffers no death or disease from environmental conditions (Environment)
Instincts
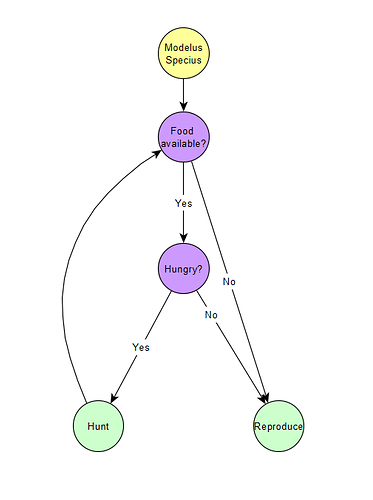
We will now introduce the basics of instincts to the system. By this I mean we will make Modelus Specius prioritize certain activities at different times. For now, Modelus Specius will always prioritize hunting over reproducing (we will expand behaviours later). He will spend as much time as he needs to hunt, and then once he has gained all the energy he needed (or all the energy that was available), he will reproduce in the remaining free time.
This does introduce a dilemma. Is Modelus Specius’ reproduction passive or active? Can it occur in parallel with hunting? This currently assumes that the body waits until all the required energy is consumed, and THEN starts replicating its cells. Couldn’t the body start replicating cells earlier with the energy it had? We will address this in a future part when we discuss passive reproduction (releasing spores) versus active reproduction (searching for and courting mates). For now we will say that even though Modelus Specius reproduces through Budding which is typically a passive method, it is an active reproduction and cannot be performed while hunting.
Anyways, the introduction of movement doesn’t affect the life cycle diagram (so none of those this part), but it does allow us to create a new diagram, the Behaviour Diagram! It’s a breakdown of how the AI of Modelus Specius operates, i.e. how he spends his time. We can make a simple behaviour tree to visualize Modelus Specius’ instincts:
So in our model, hunting ALWAYS takes priority over reproducing until there’s either no more food, the time runs out, or all the required food is hunted.
Time per Hunt
Every hunt will take a certain amount of time. Every physics class talks about the standard formula of “speed equals distance over time”. Since we want to find the time spent for each hunt, we will instead write that as:
Time per Hunt = Distance per Hunt / Speed per Hunt
Let’s imagine the scenario. Let’s say that Modelus Specius is a small, spherical blob of simple tissue about 1cm in diameter. It uses a simple method of contracting its body to swim (undulation). Let’s say it swims at 10cm/s. It always knows where the food is. Once it comes into contact with food, it instantly consumes it and receives 100% of the energy. And finally let’s say that the patch is a perfect cube that is 10m long.
Edge Cases
This part can get a little tricky with the math and the logic, but I find that it helps to imagine things by thinking of the edge cases, such as when something is at 0% or 100% of its value. Keep this in mind as we continue.
Distance per Hunt
First we must find the average distance of each hunt. Imagine there was only one Modelus Specius and one piece of food in the patch (which is a cube), how could we know the average distance between them? This is actually a common puzzle in mathematics, and the solution is surprisingly difficult (involving a double integration). Luckily, it seems that the answer is that the mean distance between two points in a cube is 66% the length of the cube, and so of course this scales with the size of the cube. Please correct me if I’m wrong on this, because this is what I understood from reading the topic and is critical to the following calculations. This is how that looks mathematically:
Distance per Hunt = (0.66 * Patch Length)
So in our 10x10x10 cube, the average distance between the Modelus Specius and the nearest (and only) piece of food is 6.6m.
NOTE
This is the first point of divergence for our algorithm between simulating microscopic and macroscopic species. Since the Microbe Stage is 2D, I’d imagine we would simulate the patches as squares not cubes, which makes the ratio 52%.
Okay, but when will a patch ever contain just one Modelus Specius and one piece of food? Now let’s imagine the opposite extreme scenario (here’s the edge cases trick I mentioned above). What if the entire volume of the patch is COMPLETELY filled, with half of the space being members of Modelus Specius and half being pieces Food, and they are evenly distributed between each other. What would the average distance be expected to be between each Modelus Specius and the nearest piece of food? Zero! Since they are literally packed shoulder to shoulder. So density REDUCES the average distance.
The Triceratops represents Modelus Specius and the Ferns the food. Imagine that they are physically filling up all the space in the patch. Notice that our model currently does NOT simulate population clustering. That is something we will address in a future part.
How do we mathematically represent density? We’ll show it as what ratio of the total volume of the patch is filled with the volume of Modelus Specius/the food. If 50% of the space in the patch is filled with food clouds, then that means the food has a population density of 50%.
So the average distance between Modelus Specius and the nearest piece of food ranges from it’s full value (at minimal density) to zero (at maximum density). Note that when I say maximum density I am referring to the densities of the predators AND the prey taking up all the space in the patch and being at a 50:50 ratio. If there is empty space in the patch, or if the ratio is imbalanced, than the average distance between predators and prey increases. This makes sense, since if the patch is 90% filled with predators and 10% filled with prey, some predators will be pretty far from the nearest prey (even if they are evenly distributed).
We can mathematically model this as:
Distance per Hunt = (0.66 * Patch Length) * (1 - (4 * Predator Population Density * Prey Population Density))
Why did I multiply the final term by 4? That’s so that when the predator and prey densities are both 50%, the average distance drops to zero. That will probably never happen in any playthrough though, due to many physical and other restraints. But it’s important so that the math works.
One last point to address. Our current equation measures the distance from the center of each Modelus Specius to the center of each food.
But Modelus specius consumes the food upon touching it, so we only care for the distance between the edges of their bodies, i.e. the red portion in the diagram below.
So, we must subtract the body radius of Modelus Specius and the “body” radius of the food from the distance, giving us the final equation of:
Distance per Hunt = (0.66 * Patch Length) * (1 - (4 * Predator Population Density * Prey Population Density)) - Predator Body Radius - Prey Body Radius
Speed per Hunt
Holy Belgium you wouldn’t think there’s so much work to just finding the average distance per hunt. Luckily the speed of the predator per hunt is very easy, since the food doesn’t try to escape. It’s just a constant we’ll apply for now that will be a trait of Modelus Specius (Swimming Speed), until we revisit swimming and hydrodynamics later. Let’s say his speed is 10cm/s, or 0.1m/s.
This gives us the following set of equations:
Distance per Hunt = (0.66 * Patch Length) * (1 - (4 * Predator Population Density * Prey Population Density)) - Predator Body Radius - Prey Body Radius
Time per Hunt = Distance per Hunt / Speed per Hunt
Time Spent Hunting
Now we must find the total time spent hunting every month. This value is PER INDIVIDUAL. Just because you have 2 lions doesn’t mean twice the time is spent hunting, because the lions will hunt simultaneously. So, we will calculate this next part by looking at the average individual member of Modelus Specius.
To find the total time spent hunting by the average individual, we just multiple the time per hunt by the number of hunts each individual needs to perform. Recall in the last part that we tracked the total amount of food consumed in the timestep. We are going to make a small tweak and change this into the food required, or in other words the hunts required. This represents the total number of hunts required by the population to feed themselves. This is important because now with movement speed, they may run out of time in the month to finish feeding!
If we divide the hunts required by the total population of predators we get the average number of prey/food that needs to be hunted by each predator, and since each hunt yields only 1 prey this also equals the number of hunts.
Hunts Required per Person = Hunts Required / Population
Required Hunting Time per Person = Hunts Required per Person * Time per Hunt
This gives us:
Distance per Hunt = (0.66 * Patch Length) * (1 - (4 * Predator Population Density * Prey Population Density)) - Predator Body Radius - Prey Body Radius
Time per Hunt = Distance per Hunt / Speed per Hunt
Hunts Required per Person = Hunts Required / Population
Required Hunting Time per Person = Hunts Required per Person * Time per Hunt
Successful Hunts
Remember that each timestep is 1 month. So we cap the maximum free time that an individual can spend hunting to 1 month. This means that if they require more than that, too bad, your time’s up. Think of it this way: If Jack needs to hunt 4 rabbits and he has 30 days to do it, but it takes 15 days to hunt each rabbit, sorry Jack you only get 2 rabbits.
Successful Hunts = Available Hunting Time per Person / Time per Hunt
Remaining Time = Free Time - Available Hunting Time per Person
This is a case that will be very unlikely to occur in our current simplified model though. It will become a more relevant concept as things get more complex.
Reproducing Time
Remember, we are tracking free time on the individual basis. So after the average individual finishes hunting, all the remaining time is used for reproduction. This gives us:
Reproducing Time per Person = Remaining Time
Which means we now tweak the births equation. Remember mating frequency gives the maximum births per month if you spend all month reproducing, but it has to be scaled down by how much time you can actually spend reproducing:
Births = Population * Available Reproducers * Mating Frequency * Reproducing Time per Person * Litter Size
Updating the Algorithm
At this point, the list of equations is growing long enough that I don’t think it’d be that helpful for me to just throw them all at you at the end of the part. If you really want it I can post it though. I’m also not really feeling the usefulness of the flow diagram. If someone wants it I can make it but otherwise I’ll ignore it for now.
Demo
However, the introduction of movement has now made the demo simulations a lot more interesting. Here is one using the conditions we discussed in this part. Note that some of these use different units in the calculations (the calculations use joules for example @hhyyrylainen ), but I’ve written them out here in easily understandable units.
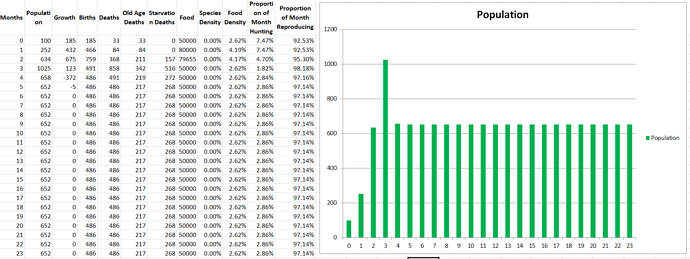
Starting Conditions
- Simulation Time = 24 months
- Modelus Specius
- Starting Population = 100
- Available Reproducers = 1.0
- Mating Frequency = 1/month
- Litter Size = 1
- Lifespan = 3 months
- Base Metabolism = 300 calories/month
- Swim Speed = 1cm/s
- Body Radius = 0.5cm
- Body Volume = 0.52cm^3
- Food
- Starting Amount = 50000
- Energy Yield = 1 calories
- Regeneration Rate = 50000/month
- Body Radius = 5cm
- Body Volume = 523.6cm^3
There are a few cool takeaways from the data. We can see that the population grows rapidly at first since food is in abundance, and then stabilizes at a lower level when shortages hit. We can also see that they are able to finish hunting so quickly that every month they still spend over 90% of their time reproducing. At first, they spend about 7% of their time hunting, but as their population increases the average distance to the food goes down and so they cut down to only spending 3% of their time hunting by the end. Also the species density is not actually 0%, it’s just a very small number that doesn’t show up. I will do a follow-up post to this one where I’ll explore different starting conditions and see what outcomes we get to better explore the simulation we’ve got going so far.
Summary
New Performance Stats
Population Density
Required Hunts
Successful Hunts
Distance per Hunt
Time per Hunt
Hunting Time per Person
Reproducing Time per Person
New Traits
Swimming Speed
Body Radius
Body Volume
Topics for Discussion
- Can the mean distance between two points in a unit cube being 0.66 be scaled with the size of the cube?
- How do we want to approximate a patch to be shaped as? A cube? A sphere?
- In microbial gameplay, will we simulate patches as 2D?
- Comments and feedback are welcome!