Nick's Auto-Evo Algorithm (Episode 1)

[NickTheNick]

Nick’s Auto-Evo Algorithm

I’m only calling it Nick’s for now since I don’t know whether it’ll work. If we decide to go with this it’ll just be the Auto-Evo Algorithm.

Table of Contents

I will update the Table of Contents as we go. Each episode will likely have to be its own thread because of how freaking much there is to discuss.

• Glossary
• Introduction
• Episode 1 – Population Algorithm
  • Part 1 – Population
  • Part 2 – Food
  • Part 3 – Movement
    • Part 3.1 - Simulation Demos
  • Part 4 – Demography
  • Part 5 – Hydrodynamics and Swimming
  • Part 6 – Competition
    • Part 6.1 – Intraspecific Competition
    • Part 6.2 – Q&A
  • Part 7 – Predation
    • Part 7.1 – Understanding Predation
  • Part 8 – Perception
    • Part 8.1 – Playtesting
    • Part 8.2 – Updates from Playtesting
  • …
• Episode 2 – Evolution Algorithm
• Episode 3 – Integration

Appendix

Glossary

There are some important terms we’ll be using throughout, so I’ll keep a record here of all of them and there meanings.

• Auto-Evo: Automatic Evolution (or Auto-Evo for short) is one of the fundamental systems of the game and one of the three pillars of the CPA System. It is an algorithm that automatically evolves species around the player to simulate a naturally evolving world.
• Compound System: The Compound System refers to the list of compounds that are present in the game and how they interact with gameplay. All entities in the game are made of compounds (representing the elements and compounds of the natural world) and can convert between each other. For example, in the Aware Stage an organism could feed on a carcass and harvest the compound “Meat”, while in the Society Stage a miner could work in a mine and harvest the compound “Iron Ore”.
• CPA System: The CPA system is an umbrella term that refers to the Compound, Auto-Evo, and Population Dynamics systems, the three most important systems of the first half of the game centered around biological evolution.
• Game Stage: Game Stages refer to the categorical divisions of the stages of the game. They are mostly categorical, since Thrive tries as much as possible to make the transitions between them seamless (though there will of course be some differences).
  • Microbe Stage: The Microbe Stage is the 1st stage of the game, where the player controls a single celled organism. The stage’s perspective is top-down. It is one of the stages that uses Auto-Evo.
  • Multicellular Stage: The Multicellular Stage is the 2nd stage of the game and begins when the player evolves into a multicellular organism. The perspective begins in top-down and transitions into being three-dimensional. With the transition between these two perspectives comes several gameplay changes, and so it’s common to specify if referring to 2D or 3D Multicellular. It is one of the stages that uses Auto-Evo.
    • Early Multicellular / 2D-Multicellular: Early Multicellular refers to the portion of the Multicellular Stage that is top-down. It mostly uses the mechanics of the Microbe Stage.
    • Late Multicellular / 3D-Multicellular: Late Multicellular refers to the portion of the Multicellular Stage that is three-dimensional. It mostly uses the mechanics of the Aware Stage.
  • Aware Stage: The Aware Stage is the 3rd stage of the game and begins when the player evolves a simple nervous system. The perspective is three-dimensional. It is one of the stages that uses Auto-Evo.
• Generation: A generation refers to a “turn” in the game. Every time you enter the editor and then return to the game, you’ve started a new generation (even though realistically each editor session represents hundreds of generations).
• Inter
• Life Activities: Life Activities refer to the various activities that comprise the lifespan of an organism. These include sleeping, eating, drinking, reproducing, socializing, migrating, etc.
• Modelus Specius: Modelus Specius is the name of the example species used throughout the design of the Auto-Evo algorithm.
• Niche: A niche is akin to a “role” of a species in an ecosystem, defined by where it lives, what it hunts, and other such factors.
• Population Dynamics: Population Dynamics is a fundamental system of the game and one of the three pillars of the CPA system. It refers to the system of simulating and monitoring the change in population of the different species in a realistic way.
• Simulation Step: This simply refers to the unit of time for simulation for the population algorithm. At the moment, this is one month. This means that all the calculations are run over the course of a month, and then repeated for however many months that we want the simulation to go for.
• Timestep: The time represented between generations is called the timestep. When a player enters the editor, does his stuff, and then returns to the game, the game fast forwards thousands or millions of years to represent the evolution that took place.

Performance Statistics

Performance Statistics are stats that help the player track the success of their species, such as population, births, deaths, starvation rate, etc. Performance statistics change from month to month.

• Population
• Births
• Deaths
• Old Age Deaths
• Energy Required
• Energy Hunted
• Energy Consumed
• Proportion Fed / Starvation Rate
• Starvation Deaths
• Spatial Population Density
• Required Hunts
• Successful Hunts
• Distance per Hunt
• Time per Hunt
• Hunting Time per Person
• Reproducing Time per Person
• Competitiveness
• Pooled Competitiveness
• Intraspecific Competition
• Caught Hunts
• Predation Deaths

Traits

Traits are stats of the species that are defined in the Organism Editor. Traits can only change through evolution, and are constant from month to month.

• Available Reproducers
• Mating Frequency
• Litter Size
• Lifespan
• Base Metabolism
• Swimming Speed
• Body Radius
• Body Volume
• Clustering
• Locomotion Type
• Muscle Area (Swimming)
• Muscle Strength (Swimming)
• Coefficient of Drag
• Frontal Surface Area
• Intraspecific Competition Rate
• Acceleration (Swimming)
• Endurance (Swimming)
• Body Mass

[NickTheNick]

Introduction

One of the biggest problems I see facing Thrive is the question of how to implement Auto-Evo, one of the fundamental concepts behind the game. Here are just some of the questions that come to mind when thinking about how to implement Auto-Evo:

• How do we design a system that automatically evolves the species alongside the player?
• How do we it in a way that stays competitive with the player’s species and other AI species?
• How do we even design a system that can look at the design of an organism and determine its survivability?
• How can the system calculate the change in survivability with a change to a certain trait?
• How do we use this system to track the changes in population of the player’s and other species based off of their traits over the generations?
• How do we make it respond effectively to changes in the environment?
• How can we do this all without melting the first computer that tries to run it?

This is a question I’ve wondered about since I joined the project many years ago, but never had any solutions for. Recently though, I feel like I’ve had some inspiration for how we can try to solve this problem. I will admit that many others have worked on this, and maybe I’m just re-treading old ground that they’ve already covered. But anyways, here’s my attempt at tackling this game’s fundamental system.

Also before we start, I’ve actually been sitting on this idea for a while and was planning to post it a while ago, but unfortunately my computer corrupted the file and I lost everything, so I’ve had to spend a while to regain the motivation to redo my work.

---

Let’s start with the basic premise that we know we want the Auto-Evo system to be designed around, taken from the current concept (with some paraphrasing).

Auto-Evo is a system that automatically evolves the species around the player. Evolution is semi-random but geared towards choosing good evolutions.

Okay, sounds simple enough, but it raises three fundamental questions:

1. How do we calculate the effect of an evolution on a species?
2. Once we calculate an effect, how do we determine how “good” it is?
3. How will this tie into the overall gameplay?

Episodes

Episode 1 will answer the first question and cover the concepts of traits, species, populations, biology, physiology, and ecology, and ultimately design a Population Algorithm to calculate the population change of a species based off of its traits and its environment. This will be the first component of the overarching Auto-Evo system.

Episode 2 will dive into the concepts and mechanics of evolution and try to answer “How do you choose how ‘good’ an evolution is”. Using the Population Algorithm from Episode 1, we will derive a method for choosing how species are evolved each generation and assessing how “good” those evolutions are to keep things competitive for the player and realistic for the simulation. This will be the second key component of building the overarching Auto-Evo system.

Episode 3 will close by addressing the third question and discussing how this Auto-Evo algorithm ties into the game at large. It will also address how a slightly modified version of Auto-Evo will be used for assessing the success of the player’s species based off of a combination of the player’s design of their species in the editor, as well as their performance with their species during gameplay.

Strategies

To make the construction of this algorithm easier, we will have to use several strategies in its design:

Averages . Our goal will be to measure the success of the average individual from every species. Wherever possible, we will use averages to calculate or represent the statistics of the members of the species instead of individual data points. We will tend to treat the species as a cohesive unit. We won’t care about whether one member catches a lot of food, and one member doesn’t catch enough, we’ll only look at the average food caught between them. We also don’t look at whether they specifically win on a certain hunt or lose on another certain hunt, only the average success ratio across all hunts. Of course, when there are important details that should not be simply “averaged out”, we will consider them (like for example a human could not starve all year and then eat all their calories on December 31st).

Proportional Estimations . Some qualities can be hard to describe numerically to plug into an algorithm. How do you quantify something like the aggressiveness of a species with a number? Wherever possible, we will use proportions to estimate these traits. In the case of aggression, for example, you could model it on a scale from 0 to 1.0, where 0 represents engaging in an aggressive interaction 0% of the time towards another individual, while 1.0 means engaging aggressively in 100% of interactions with others. An aggressiveness of 0.5 would mean engaging in aggression 50% of the time.

Life Activities . If you think about the life of any organism, it’s essentially just a compilation of time spent doing all the different activities of life (aka “Life Activities” as we’ll call them). These include sleeping, eating, drinking, reproducing, socializing, migrating, etc. Each of these activities pose their own challenges to species, which can lead evolution to evolve traits adapting to each one. It might be hard to imagine how a longer leg would affect the survivability of a species when looking at the effect on its entire life all at once, but if you break it down it’s much easier to imagine how a longer leg would affect its individual activities such as its hunting, its migrating, its drinking, and more. Additionally, each of these activities can be completed at differing levels of performance. As a result, if we want to look at the overall performance of a species, we can start by looking at the performance across each of the different life activities it engages in and factoring them all into an overall performance score.

Building from the Basics . This will be a complicated algorithm with many variables, and it can be overwhelming to try and design an entire algorithm like this all at once. Instead, we’ll begin by making as many assumptions as possible and creating the most simplified scenario possible with the least number of unknown variables. We will call this example species Modelus Specius . This gives us something incredibly basic to start with to help us think about how to build up the framework for our algorithm. Here are some example assumptions for the initial scenario:

• Members of Modelus Specius can instantly detect, teleport to, catch, and consume food
• Consumption of food always yields 100% of the energy in it
• Members of Modelus Specius do not age. They spawn as fully capable individuals that immediately begin functioning independently.

As you might imagine, this initial scenario will be extremely unrealistic, but luckily that doesn’t matter. We will one by one introduce all the realistic elements as we work towards making the final algorithm. Notice that it doesn’t take into account perception or camouflage (they instantly detect the food), movement (they teleport to the food), or metabolism (100% of food turned into energy). This means we’ll start by essentially just creating a population growth equation, and then incrementally introduce features like perception and metabolism and socialization to flesh it out into a realistic and accurate algorithm.

By doing it step by step in this way, we hopefully make it easier for ourselves to understand, to make sure it’s realistic, and in the end gives us the Auto-Evo system that we want!

Coincidentally, the initial simplified scenario is kind of similar to the beginnings of the 3D Multicellular stage. The starting organisms in the 3D Multicellular stage are very basic and cannot engage in many advanced activities (such as mating rituals or cooperative hunting), sort of like our starting simplified model. The process of making the Auto-Evo algorithm more complex by one by one introducing the elements of evolution will be sort of similar to the progression of the player through the Multicellular and Aware stages (only sort of, some parts are obviously very different like the teleportation).

Bundles of Statistics . At the end of the day, we always need to remember that the species and organisms in Thrive are just a collection of statistics, and we can always treat them as such whenever we need to. If it might seem daunting at first to build this algorithm, such as when we want to calculate running speed or the daily metabolism or the force of a bite, we should remember that the data for all of this will be defined in the Organism Editor. Stats like mass, surface area, muscle size, density, shape, bone layout, and more will all be available to us. Our job is simply to take this data and process it in a way that produces a realistic enough outcome.

Let’s Get Started

That’s it for the introduction. In the next post we’ll start with episode 1 and take the first steps to building the algorithm!

[hhyyrylainen]

@NickTheNick

• 2D-Multicellular : 2D-Multicellular refers to the portion of the Multicellular Stage that is top-down. It mostly uses the mechanics of the Microbe Stage.
• 3D-Multicellular : 3D-Multicellular refers to the portion of the Multicellular Stage that is three-dimensional. It mostly uses the mechanics of the Aware Stage.

I’ve been using the terms “early multicellular” and “late multicellular” to refer to these two parts of the multicellular stage. I’m not sure which I prefer.

Here’s my kinda technical post about how I imagine the auto-evo to be implemented:

New CPA system with auto evo

I feel like the species should attempt to mimic natural selection instead of the energy balance being used to update the population. I guess this system could also do that with the different species emerging when some die out. But I’d prefer a more complex equation for determining the “effectiveness” of some mutation. So merging that with my current understanding of the goals of auto evo it would work something like this: when the player enters the stage (either from the editor or a new game) …

That basically touches on the technical side of things, but lefts completely open what kind of fitness evaluation function we should make. I didn’t have time to properly read this thread yet, but I wanted to post this right now.

Also @tjwhale you should link / post your auto-evo stuff

[NickTheNick]

@hhyyrylainen

I’ve been using the terms “early multicellular” and “late multicellular” to refer to these two parts of the multicellular stage. I’m not sure which I prefer.

Here’s my kinda technical post about how I imagine the auto-evo to be implemented:

Ah yeah those are good names I’ll use those.

@hhyyrylainen

Here’s my kinda technical post about how I imagine the auto-evo to be implemented:

Yeah I pretty much agree with your idea on how to model auto-evo. When I post the next episode you’ll see what I mean.

Picture

From the thread you linked, that is the part I’ll mostly be working on at first. It’ll all be about how to calculate the population dynamics of the species. I’ll explain it more when I post the first episode.

[NickTheNick]

Episode 1 – Population Algorithm

“How does one calculate the effect of an evolution on a species?”

Part 1: Population

Before we do anything else, the very first thing we must determine is how to calculate the effect of any change, mutation, or evolution on a species. Once we figure that out, we can proceed to Episode 2, where we calculate several different evolutions for a species, and then choose the best one.

To address this first question, the answer lies in population. Population is the ultimate success metric for life, since population growth is life’s ultimate goal. Evolution by natural selection is rooted in the principle that the guiding force of life is to propagate your DNA, and the medium of DNA is population. Have more offspring, and you have more copies of your DNA. Ensure that your offspring have more offspring, and you have further copies of your DNA still. Even the acquisition of food is only a means to the end of sustaining and multiplying your population. Population growth and decline is also what determines the appearance and disappearance (extinction) of species. As such, we can see that population is the central metric to track for a species to measure its performance, a convention already in wide use in modern science.

So, within one paragraph we already know the conclusion of this episode: You calculate the effect of an evolution on a species by seeing how it changes its population in future generations. In Episode 2, we will look at how you can assign several different evolutions to a species, calculate which one produces the greatest growth in population, and choose that one as the mutation chosen by Auto-Evo.

However, it’s not as easy as just saying “by seeing how it changes its population in future generations”. How exactly does that work? There is a lot of work still left before we can move to the next episode, since the rest of this episode is all about figuring out how exactly any given evolution will change the population. We will need to figure out exactly what stats of the creature will cause exactly what changes to their population and by which exact mathematical relationships. This might seem difficult at first but remember, we have several strategies described earlier to help make this process easier.

Mathematical Aside

Discrete vs Continuous Modelling?

Before we can begin creating the algorithm, we must answer a fundamental mathematical question: Do we make a discrete or continuous model?

Discrete Model

A discrete model assumes that changes only take place at specific intervals. For example, a discrete model for population growth would take the current population, and an annual growth rate, and tell you what the population would be after 1 year:

Population at Next Year = Growth Rate * Population at Current Year

For example: 110 = 1.1 * 100

We can also rewrite this equation using function notation:

n[t+1] = R * n[t]

Where:
t is the current year
t+1 is the next year
n is the population
n[t] is population at the current year
n[t+1] is the population at the next year
R is the growth rate

If R is 1.1, that is equivalent to 110%, or that the population is growing by 10% every year. An R of 0.9 is equal to 90% and means that the population is shrinking by 10% every year. An R of 1.0 means a growth rate of 100% which means that the population is staying exactly the same (such as if exactly as many organisms died as were born).

Benefits

The benefit of discrete models is that they are simple and easy to understand and do the math for, as they are the usual way we do simple math at the high school level or in everyday situations. It also makes it pretty easy to track information at each timestep to monitor changes in the environment.

Drawbacks

One consequence of this discrete method though is that it assumes that none of the births in that year birthed any of their own. Its equivalent to saying that all the births happened exactly at the last moment of the year, or all right at the beginning and then no other births for the rest of the year.

Why is calculating at specific intervals an issue? It’s because this leads to problems no matter how large or small we make the time interval. If we make the interval too large such as 1 year, this could lead to less realistic outcomes. Perhaps the species has very short lives and within a year they could have offspring and then those offspring could have their own offspring. However, a 1 year interval wouldn’t allow for that, since the offspring would have to wait a minimum of 1 year before the calculation could run again. If we make the interval too small, such as 1 week, this could lead to very computer intensive calculations that would slow down the game. The game would have to run the entire Auto-Evo calculation 52 times just to simulate growth over a single year, and that’s only for one species!

Continuous Model

The alternative to this are continuous models. This is where you calculate a continuous rate of change over the interval, meaning that offspring born within a year could have their own offspring. For example, a continuous model for population growth will give us the change in the population at any given instantaneous moment:

Rate of Change of Population at Current Moment = Growth Rate * Population at Current Moment

Or with proper function notation:

dn[t] / dt = R * n[t]

Where:
dn[t] / dt is the change in population at a given instant
R is the growth rate
n[t] is the population at a given instant

You then would calculate this multiple times to find the overall change of a population over 1 year, and it would give you a slightly different answer than a discrete model, but still pretty close. The difference could even be larger based on the parameters.

Drawbacks

What are the downsides of continuous modelling? Well, how do you use equation that gives population change at any given instant to calculate the total change over an entire year? Surprise surprise, to anyone who hasn’t done this in college, its calculus. It means our model would have to involve a lot of calculus, and that would make things a LOT more challenging (especially for me since it’s been a few years since I’ve studied calculus).

Which is the Better Model?

So the question is, do we use a discrete model, or a continuous one?

My vote is for a discrete model. It’ll save us the headaches of constantly having to work with calculus, and we can hopefully try to strike a balance with the time intervals where it’s not too long and not too short to produce any of the problems listed above. It also allows us to easily track information between time intervals and display these to the player.

The interval that I think would be the best balance is 1 month per interval. Most species on Earth have lifespans that are at least 1 month long. In fact, almost every exception to this rule is in microbial organisms. Perhaps we can make two different algorithms, with one that uses 1 month timesteps and one that uses smaller timesteps? The smaller timestep model would only be used for microbial life, which wouldn’t create any overlap since all microbial life stops being simulated during the 2D-3D transition of the Multicellular Stage.

Initial Algorithm

Assuming we create a discrete model, we can finally get started on the algorithm.

Let’s create a list of all the assumptions we are making to create our extremely simple and easy to understand scenario.

Current Assumptions

• Modelus Specius is a flat, tiny, simple, jelly-like organism that lives at the bottom of the ocean.
• The species is always fully satiated with food and water (Nutrition)
• The species is equally distributed/dispersed across the world (Demographics)
• The planet is one giant ocean of equal pressure water that is equally accessible to the player (Geography/Terrain)
• Members can reproduce as many times as they want, instantly, with no pregnancy/gestation period. (Reproduction)
• The species reproduces via asexual reproduction, spawning fully developed offspring that can themselves immediately begin reproducing. (Mating)
• The species does not change in physiology as they age (Aging/Ontogeny)
• The species is fully aquatic (Terrestriality)
• Members of the species are solitary and do not cooperate with other species members in any way. (Cooperation/Sociality)
• The species has no parental instincts, and will immediately abandon offspring (Parenting)
• The species is perfectly adapted to its environment and suffers no death or disease from environmental conditions (Environment)

In future parts, we will always have a list of all current assumptions at the BEGINNING of the post, and we will explain what assumptions are being “peeled away” (replaced with realistic mechanics) in that part. This will hopefully ensure we understand the algorithm every step of the way.

Using our simple model, here’s a simple place to start. The following equation calculates the change in population over one timestep (1 month):

Population = Initial Population + Births - Deaths

OR

P = Pi + B – D

Okay, easy enough. Now let’s break down how to calculate Births (B) and Deaths (D).

Births

What determines how many births there are in a timestep?

First we look at how many individuals CAN reproduce (Available Reproducers). For example, in the human population this would be around 50%, since only females can reproduce. However, in Modelus Specius, there are no sexes and all members are capable of asexual reproduction, thus making the available reproducers 100% or 1.0.

Then, of those that can reproduce, how frequently do they actually reproduce (Mating Frequency)? In some species, this is influenced by factors such as sexual competition. However, in our simple Modelus Specius, this is only limited by how often they can reproduce within physical limits. In fact Modelus Specius spends 100% of its time just reproducing. The only thing that limits it is how fast the cells can replicate to reach double their original number and spawn an offspring. This means Modelus Specius uses Budding to reproduce. Let’s say that the cells in Modelus Specius replicate fast enough to allow it to reproduce once per month.

Then, when these members reproduce, we need to know how many offspring are produced (Litter Size). Since Modelus Specius reproduces by Budding, we’ll say it only produces 1 offspring.

Thus we can break Births down into:

Births = Initial Population * Available Reproducers * Mating Frequency * Litter Size

And with our example numbers

Deaths

At this point, our model is so simple that members of Modelus Specius only die from old age. Yes, I know, what does it mean to die of old age? For now, we’ll keep this old age model extremely simple and simply say it’s natural diseases that occur and kill organisms after a certain amount of time. In a later part we’ll revisit it and replace it with a realistic model of ontogeny and aging.

Let’s say that Modelus Specius has an average lifespan of 3 months. Some die at 2 months, some live to 5 months, but on average they live 3. We can then assume that with a starting population of 100 newborns, 100% of them will die in 3 months, and 33% of them will have died by the first month. At the moment we will not be keeping track of multiple generations. Also, in real life it’s more common for deaths from old age to increase in likelihood when you get older, but we are also ignoring that for the moment. From this we get:

Deaths = Initial Population * 1 / Lifespan

Updating the Equation

Now plugging these back into our equation, we get:

Births = Initial Population * Available Reproducers * Mating Frequency * Litter Size
Deaths = Initial Population * 1 / Lifespan
Population = Initial Population + Births - Deaths

Visualizing the Algorithm

As we progress through the series, we NEED to keep track of our algorithm as we build it up. This is so that we always are able to understand it as we’re building it and we never start to get confused by how complicated it is. To help with this, I think it’s better to visualize it in several different methods. We will use these methods throughout the series as we build the algorithm.

Equations

The first method of representing the algorithm is simply to write out the list of equations we are using. This is what we have so far:

Births = Initial Population * Available Reproducers * Mating Frequency * Litter Size
Deaths = Initial Population * 1 / Lifespan
Population = Initial Population + Births - Deaths

Another way of looking at the algorithm is to draw a visual diagram of what is happening with the species under Auto-Evo. The two diagrams we’ll use are the Life Cycle Diagram, and the Flow Diagram.

Life Cycle Diagram

The Life Cycle Diagram shows the order of events in the lifespan of an organism of the species. Here is the typical Life Cycle Diagram used in biology:

Notice how from one generation to the next, there are actually several steps at which members can die and natural selection can do its work. Not all of natural selection is involved in whether you survive to adulthood, which is the part people usually think of. There is also the “competition” of which adults get to reproduce (especially if they need to find mates, which is sexual selection), how fertile and successful those reproducing adults are, and how successful the gametes are in fertilizing. However, most of these are irrelevant in our current simple model.

A cool benefit of this diagram is that it also can show us what order calculations are done by the algorithm. Let’s rewrite the diagram to show our current algorithm.

We start with the initial population of the generation. Some of them birth new offspring, and some of them die of old age. Some can birth an offspring and then die of old age. Once we factor in the births and deaths we get the population of the next timestep.

However, there is one problem with this. The order of calculation is very important. What if you die of old age before you reproduce? The current model does not allow for that. This might seem trivial now, but it will become very important in the future when an individual might die of starvation before they can give birth, which is an important factor of natural selection. Let’s re-order our equations to first kill off all the members who are dying of old age, and THEN have the survivors reproduce.

Deaths = Initial Population * 1 / Lifespan
Intermediary Population = Initial Population - Deaths
Births = Intermediary Population * Available Reproducers * Mating Frequency * Litter Size
Population = Intermediary Population + Births

What does this now look like?

Flow Diagram

Another way to visualize the data is with a flow diagram. This simply shows all the different factors that increase (inflows) and decrease (outflows) the population every timestep. It can even be expanded to show what variables affect each of these flows. Here’s a simple mockup:

I have a feeling this one will not be as helpful once the model starts getting more complex, but I’ll keep it around for now.

Demo

I think Excel is good for visualizing the data, but ultimately a scripting language like Python is needed to make a demo of the algorithm (some functions are just not possible or too complicated in excel). Using Python, I made a script to model the algorithm we have so far. At the end it spits out a monthly report of the environment as a CSV file.

Starting Conditions

• Simulation Time = 24 months
• Modelus Specius
  • Starting Population = 100
  • Available Reproducers = 1.0
  • Mating Frequency = 1/month
  • Litter Size = 1
  • Lifespan = 3 months

Notice that the population grows exponentially, since there is nothing to limit it. In future parts we will fix this by introducing more elements of the natural environment to produce a more realistic outcome.

---

Summary

Every part will end with the Summary. The summary will have two lists and a compilation of all the unanswered questions that need to be addressed for that part. This is to keep a running tally of all new stats we add to the algorithm and what design decisions need to be discussed next. The first will be a list of any new Performance Statistics introduced in that part. These are stats that help the player track the success of their species, such as population, births, deaths, starvation rate, etc. Performance statistics change from month to month. The second is a list of Traits introduced in that part. These are stats of the species that are defined in the OE. Traits can only change through evolution, and are constant from month to month. The first post will have an appendix to keep a record of all Performance Statistics and Traits as they are added.

Performance Statistics
Population
Births
Deaths
Old Age Deaths

Traits
Available Reproducers
Mating Frequency
Litter Size
Lifespan

Topics for Discussion

• Do we go with a Discrete or Continuous Model?

---

Finally, I’d just like to take a minute to point out how incredibly useful I think it is that we are starting with such a simplified model. Even with such a simplified starting model, look how complicated things have already gotten! We’ve discussed discrete versus continuous mathematical models, calculus, different types of natural selection, different types of mathematical modelling of population growth, different visual representations of the auto-evo process, and introduced various variables to construct our initial equation, and this is only the first part of the first episode! Clearly we will have to take things slowly and make sure everything makes sense and fits together along the way.

[Narotiza]

A small question: why do we need to calculate a species’ population within such small timesteps? Going through an editor cycle represents millions of years passing, and dividing all that up into something as small as months in order to figure out how an adaptation affects population seems a little inefficient.
I see how it could be interesting to see populations subtly change through the seasons as you play as a more long-lived organism. But I don’t think any organism gameplay will last much longer than a single generation, and for the most part species populations seem like they’d be mostly static throughout the gameplay phases of the game.

[NickTheNick]

Good question, and it’s something that is explained fully in Episode 2, but here’s a quick overview.

The current population algorithm is not actually to use to calculate how the population will change over the many many months that there would be in millions of years of evolution. It’s only so that we have a way of measuring the “Performance” or “Fitness” of a species, since we’re defining fitness as that which gives the biggest boost to population growth.

The idea is we assign a mutation to a species, and then look at how that would affect its population growth over a simulation of X months (let’s say 120).

For example, say you have Species A. You create four sample groups of Species A, and assign a random mutation to each one (all these numbers are random):

• Increase leg length by 10%
• Increase digestive ability of stomach by 25%
• Increase shoulder width by 20%
• No mutation

Then for each of these sample groups, you run the Population Algorithm on them for 120 months to see how much it changes the population. The sample group that has the greatest growth is the winner.

The winner has its mutation chosen and applied to the species, and the game fast-forwards millions of years to the next generation of gameplay. If the winner was the group with no mutation, then the species does not evolve that generation.

It’s sort of like we have a car and we are designing a little test-track for it to drive on to simulate driving in the real world. Then we make changes to the car and see how it affects its performance on the test track to decide whether the change was good or bad for when it goes into the real world.

[NickTheNick]

Part 2: Food

The ultimate and eternal goal of life might be reproduction, but the means to that is acquiring food. I can’t blame them, without it, you’re dead.

I know that the last part was very lengthy, so this one will be pretty brief. Recall the list of assumptions in the previous part. One thing I like to imagine as we work on this algorithm is the idea of cutting down that list of assumptions like peeling the layers of an onion. Every assumption we peel off takes us one step closer to the final, realistic algorithm, or the center of the onion. But we have to be careful and do it properly if we don’t want to break down into tears.

Remember in the demo from the last part that the population grew exponentially forever? In this part, we’ll start to address that by introducing the main limiter of life: Food.

From our current list of assumptions, here is the assumption we will address this part:

• Modelus Specius is a flat, tiny, simple, jelly-like organism that lives at the bottom of the ocean.
• The species is always fully satiated with food and water (Nutrition)
  • Which we will replace with:
  • Members of the species can instantly perceive food regardless of distance (Perception)
  • Members of the species can instantly teleport to perceived food (Movement)
  • Members of the species can completely consume the food and gain 100% of the energy. (Hunting/Metabolism)
• The species is equally distributed/dispersed across the world (Demographics)
• The planet is one giant ocean of equal pressure water that is equally accessible to the player (Geography/Terrain)
• Members can reproduce as many times as they want, instantly, with no pregnancy/gestation period. (Reproduction)
• The species reproduces via asexual reproduction, spawning fully developed offspring that can themselves immediately begin reproducing. (Mating)
• The species does not change in physiology as they age (Aging/Ontogeny)
• The species is fully aquatic (Terrestriality)
• Members of the species are solitary and do not cooperate with other species members in any way. (Cooperation/Sociality)
• The species has no parental instincts, and will immediately abandon offspring (Parenting)
• The species is perfectly adapted to its environment and suffers no death or disease from environmental conditions (Environment)

Calories

The basic unit of measuring food and consumption will be the calorie (specifically the food calorie or kilocalorie). It can be used to measure the energy yielded from food and the energy needed by organisms to survive and do things. Every month, the species will have a total number of calories they need to eat. If they fall short of that number, then they lose some members to starvation. First let’s calculate the calories needed by the species.

Every species member will have a Base Metabolism, which refers to the standard amount of calories they will burn on a typical day just by existing. This is equivalent to a concept called Basal Metabolic Rate in biology, but is not exactly the same since our scenario is still so simplistic. Also, since our organisms are so simple, their base metabolism will not fluctuate day by day, since whereas in real life activities like hunting, hibernating, or reproducing can drastically change the amount of calories you burn.

Modelus Specius is a very small and simple organism, so we will give him a base metabolism of 10 calories per day, which comes out to 300 calories per month. Then we multiply this by the total population at a given timestep, and that gives us the total number of calories needed by the species at a timestep.

Calories Required = Base Metabolism * Population

Starvation

Since we are using averages, let’s say that the ratio of calories consumed to the calories required represents the proportion of the overall population that is fed (Proportion Fed). The species only eats as much as they require and no more, so Proportion Fed is capped at 1.00.

Say the species only consumes 75% of the calories they need. This makes the Proportion Fed 0.75. This could mean that 75% of the population receives all the calories they need and suffer no health consequences, and 25% receive no calories and die of starvation. However, this could also mean that 100% of the population only receives 75% of the calories they need, and as a result of the health consequences (aka diseases) they get from this, 25% of the population dies. So, in a way, these deaths are theoretically from starvation AND starvation-induced disease. The statistic could also represent any range of possibilities in between.

Let’s show how this would be represented mathematically:

Proportion Fed = Calories Consumed / Calories Required
Deaths from Starvation = Population * (1.00 – Proportion Fed)

Updating the Algorithm

Recall the current equations:

Deaths = Initial Population * 1 / Lifespan
Intermediary Population = Initial Population - Deaths
Births = Intermediary Population * Available Reproducers * Mating Frequency * Litter Size
Population = Intermediary Population + Births

Now we’ll add in deaths from starvation. Remember, the order of calculation is very important, so this is the order we will follow:

• We start with the current population of the species
• Next, all of the old species members die of old age
• Next, all of the younger species members feed, and those who don’t die of starvation
• Finally, all of the surviving species members reproduce

This is how that looks like:

Old Age Deaths = Initial Population * 1 / Lifespan
Intermediary Population 1 = Initial Population - Old Age Deaths

Proportion Fed = Calories Consumed / Calories Required
Deaths from Starvation = Population * (1.00 – Proportion Fed)
Intermediary Population 2 = Intermediary Population 1 - Starvation Deaths

Births = Intermediary Population 2 * Available Reproducers * Mating Frequency * Litter Size
Population = Intermediary Population + Births

And let’s visualize this with a Life Cycle Diagram:

Straightforward enough. There is one last thing we need to implement though, and that is where the calories come from. There are 3 different scenarios we can have.

Infinite Food

Food can be infinite, in which case we don’t track how much food is being consumed every timestep. We only care about the calories it provides the species. This essentially produces the exponential growth we saw in Part 1 since there is nothing to limit growth. This won’t be the approach we take.

Finite Non-Renewable Food

Food can be a limited/finite source. Eventually the calories will run out and the species will go extinct through starvation. This is also not the approach we will take, since it means the species will go extinct very quickly.

Finite Renewable Food

Finally, we can have food be a limited but renewing source. THIS is the approach we will go with, since it best simulates an ecosystem until we can start later adding in details like autotrophy and predation.

At this point, imagine the food to be individual little clouds of glucose floating in the water. We’ll say that each one yields 10 calories when consumed, and that the environment begins with 50,000 of them at the start of the simulation. Now let’s model this in the algorithm:

First, we calculate the total calories available from the food.

Calories Available = Food Amount * Calories per Food
Calories Required = Base Metabolism * Population
Calories Consumed = Calories Required OR Calories Available    #Whichever is smaller

Food Consumed = Calories Consumed / Calories per Food
Food = Initial Food - Food Consumed + Food Generated

Proportion Fed = Calories Consumed / Calories Required
...

And from this point on we’ve got the equations you saw above.

Calories Consumed will be capped by the total amount of calories available in the environment. Also, as the calories are consumed the amount of food is reduced. The food is also replenished at a steady rate every month (Food Generated).

Demo

With all of the equations finished, let’s plug into the demo and see the outcome.

Starting Conditions

• Simulation Time = 24 months
• Modelus Specius
  • Starting Population = 100
  • Available Reproducers = 1.0
  • Mating Frequency = 1/month
  • Litter Size = 1
  • Lifespan = 3 months
  • Base Metabolism = 300 calories/month
• Food
  • Starting Amount = 50000
  • Calorie Yield = 10 calories
  • Regeneration Rate = 50000/month

There we go! Now the population is limited by the amount of food that is available in the environment. Notice that at first there is so much food available that Modelus Specius essentially grows exponentially. However, once the surplus runs out, famine hits and starvation rates cause the population to fall and stabilize at a much lower level. Interestingly, this is the furthest that most mathematical modelling of populations goes (except they sort of incorporate food with habitat space and other factors into an overall “carrying capacity” resource). So, from this point on, we are venturing into uncharted territories with the algorithm. It’s exciting to see how things develop!

This current model for food does assume many things to make it simple, and we will expand on these in the future to make the algorithm more realistic. These include:

• Food is equally distributed between all species members with no competition
• All the required food could be eaten on the last possible day of the month and still meet the monthly quota, instead of having to be eaten at regular intervals
• No discrimination between food groups for calorie intake
• There is no such thing as storing food either physically or through fat reserves

---

Summary

New Performance Statistics

Calories Required
Calories Consumed
Proportion Fed / Starvation Rate
Starvation Deaths

New Traits

Base Metabolism

Topics for Discussion

Suggestions and feedback are welcome!

[hhyyrylainen]

@NickTheNick

Calories

May I suggest that we use KJ as the (primary) unit of energy, to better achieve the goal of being scientific. EU regulation 1169/2011 says that all food packaging needs to have the energy content said (first) in terms of kilo joules.

I’m liking this series so far. Recapping all the variables (showing the whole algorithm) is very nice. Hopefully at the end there’ll be some algorithm that can be quite easily converted into code.

@NickTheNick

Food is equally distributed between all species members with no competition

Is this correct? Shouldn’t there be competition between species, as our model will act on a per species approach. Or are we going to get there in a future post?

[NickTheNick]

@hhyyrylainen

May I suggest that we use KJ as the (primary) unit of energy, to better achieve the goal of being scientific. EU regulation 1169/2011 says that all food packaging needs to have the energy content said (first) in terms of kilo joules.

I’m liking this series so far. Recapping all the variables (showing the whole algorithm) is very nice. Hopefully at the end there’ll be some algorithm that can be quite easily converted into code.

Sure yeah we could make that change.

I’m making a Python script of the algorithm in parallel with posting the parts (I’m using it for posting the demos), so whenever anyone is interested I can send them a download link so they can see how it all works together.

@hhyyrylainen

Is this correct? Shouldn’t there be competition between species, as our model will act on a per species approach. Or are we going to get there in a future post?

By this I mean there is no intraspecific competition, i.e. that members of Modelus Specius don’t compete with each other for the food. They consume it on a first come, first served basis and leave leftovers for whoever’s after them. In one of the next few parts I’ll introduce how to replace this with more realistic models.

---

Also to anyone reading the thread, all feedback is welcome! Don’t feel daunted by not yet having read the full post. I’ve got the next part ready but I’ll wait a bit to give people a chance to give input on everything so far.

[NickTheNick]

FOREWORD
Before I post the next part, I want to point out I had to spend a few hours debugging the auto-evo script because of the additions from this part. I finally figured out it was because of inconsistencies in the units. Some measurements were per month (like mating frequency), some were per second (like speed), and some were per individual while others were per the entire species. So I went through all the code and converted everything into SI units (the standard for science), and managed to finally fix it. It doesn’t really apply to you as the reader too much, but you might notice small inconsistencies with the numbers in Parts 1 and 2 with the future parts, and that’s because of this conversion. Anyways, on to the part!

Part 3: Movement

So far, the species has been hunting instantaneously, and therefore spending all of its actual time reproducing. Thus it was only limited in its growth by how often it could reproduce based on physical limits. Now let’s take the first step to fixing that and introduce some time dependence on hunting. This is the first step towards differentiating between the different life activities of the species and time spent between them.

From our current list of assumptions, here is the assumption we will address this part:

• Modelus Specius is a flat, tiny, simple, jelly-like organism that lives at the bottom of the ocean.
• Members of the species can instantly perceive food regardless of distance (Perception)
• Members of the species can instantly teleport to perceived food (Movement)
  • Which we will remove and replace by actually tracking the time taken to reach food.
• Members of the species can completely consume the food and gain 100% of the energy. (Hunting/Metabolism)
• The species is equally distributed/dispersed across the world (Demographics)
• The planet is one giant ocean of equal pressure water that is equally accessible to the player (Geography/Terrain)
• Modelus Specius is the only species on the planet (Ecology)
• Members can reproduce as many times as they want, instantly, with no pregnancy/gestation period. (Reproduction)
• The species reproduces via asexual reproduction, spawning fully developed offspring that can themselves immediately begin reproducing. (Mating)
• The species does not change in physiology as they age (Aging/Ontogeny)
• The species is fully aquatic (Terrestriality)
• Members of the species are solitary and do not cooperate with other species members in any way. (Cooperation/Sociality)
• The species has no parental instincts, and will immediately abandon offspring (Parenting)
• The species is perfectly adapted to its environment and suffers no death or disease from environmental conditions (Environment)

Instincts

We will now introduce the basics of instincts to the system. By this I mean we will make Modelus Specius prioritize certain activities at different times. For now, Modelus Specius will always prioritize hunting over reproducing (we will expand behaviours later). He will spend as much time as he needs to hunt, and then once he has gained all the energy he needed (or all the energy that was available), he will reproduce in the remaining free time.

This does introduce a dilemma. Is Modelus Specius’ reproduction passive or active? Can it occur in parallel with hunting? This currently assumes that the body waits until all the required energy is consumed, and THEN starts replicating its cells. Couldn’t the body start replicating cells earlier with the energy it had? We will address this in a future part when we discuss passive reproduction (releasing spores) versus active reproduction (searching for and courting mates). For now we will say that even though Modelus Specius reproduces through Budding which is typically a passive method, it is an active reproduction and cannot be performed while hunting.

Anyways, the introduction of movement doesn’t affect the life cycle diagram (so none of those this part), but it does allow us to create a new diagram, the Behaviour Diagram! It’s a breakdown of how the AI of Modelus Specius operates, i.e. how he spends his time. We can make a simple behaviour tree to visualize Modelus Specius’ instincts:

So in our model, hunting ALWAYS takes priority over reproducing until there’s either no more food, the time runs out, or all the required food is hunted.

Time per Hunt

Every hunt will take a certain amount of time. Every physics class talks about the standard formula of “speed equals distance over time”. Since we want to find the time spent for each hunt, we will instead write that as:

Time per Hunt = Distance per Hunt / Speed per Hunt

Let’s imagine the scenario. Let’s say that Modelus Specius is a small, spherical blob of simple tissue about 1cm in diameter. It uses a simple method of contracting its body to swim (undulation). Let’s say it swims at 10cm/s. It always knows where the food is. Once it comes into contact with food, it instantly consumes it and receives 100% of the energy. And finally let’s say that the patch is a perfect cube that is 10m long.

Edge Cases

This part can get a little tricky with the math and the logic, but I find that it helps to imagine things by thinking of the edge cases, such as when something is at 0% or 100% of its value. Keep this in mind as we continue.

Distance per Hunt

First we must find the average distance of each hunt. Imagine there was only one Modelus Specius and one piece of food in the patch (which is a cube), how could we know the average distance between them? This is actually a common puzzle in mathematics, and the solution is surprisingly difficult (involving a double integration). Luckily, it seems that the answer is that the mean distance between two points in a cube is 66% the length of the cube, and so of course this scales with the size of the cube. Please correct me if I’m wrong on this, because this is what I understood from reading the topic and is critical to the following calculations. This is how that looks mathematically:

Distance per Hunt = (0.66 * Patch Length) 

So in our 10x10x10 cube, the average distance between the Modelus Specius and the nearest (and only) piece of food is 6.6m.

NOTE
This is the first point of divergence for our algorithm between simulating microscopic and macroscopic species. Since the Microbe Stage is 2D, I’d imagine we would simulate the patches as squares not cubes, which makes the ratio 52%.

Okay, but when will a patch ever contain just one Modelus Specius and one piece of food? Now let’s imagine the opposite extreme scenario (here’s the edge cases trick I mentioned above). What if the entire volume of the patch is COMPLETELY filled, with half of the space being members of Modelus Specius and half being pieces Food, and they are evenly distributed between each other. What would the average distance be expected to be between each Modelus Specius and the nearest piece of food? Zero! Since they are literally packed shoulder to shoulder. So density REDUCES the average distance.

The Triceratops represents Modelus Specius and the Ferns the food. Imagine that they are physically filling up all the space in the patch. Notice that our model currently does NOT simulate population clustering. That is something we will address in a future part.

How do we mathematically represent density? We’ll show it as what ratio of the total volume of the patch is filled with the volume of Modelus Specius/the food. If 50% of the space in the patch is filled with food clouds, then that means the food has a population density of 50%.

So the average distance between Modelus Specius and the nearest piece of food ranges from it’s full value (at minimal density) to zero (at maximum density). Note that when I say maximum density I am referring to the densities of the predators AND the prey taking up all the space in the patch and being at a 50:50 ratio. If there is empty space in the patch, or if the ratio is imbalanced, than the average distance between predators and prey increases. This makes sense, since if the patch is 90% filled with predators and 10% filled with prey, some predators will be pretty far from the nearest prey (even if they are evenly distributed).

We can mathematically model this as:

Distance per Hunt = (0.66 * Patch Length) * (1 - (4 * Predator Population Density * Prey Population Density)) 

Why did I multiply the final term by 4? That’s so that when the predator and prey densities are both 50%, the average distance drops to zero. That will probably never happen in any playthrough though, due to many physical and other restraints. But it’s important so that the math works.

One last point to address. Our current equation measures the distance from the center of each Modelus Specius to the center of each food.

But Modelus specius consumes the food upon touching it, so we only care for the distance between the edges of their bodies, i.e. the red portion in the diagram below.

So, we must subtract the body radius of Modelus Specius and the “body” radius of the food from the distance, giving us the final equation of:

Distance per Hunt = (0.66 * Patch Length) * (1 - (4 * Predator Population Density * Prey Population Density)) - Predator Body Radius - Prey Body Radius

Speed per Hunt

Holy Belgium you wouldn’t think there’s so much work to just finding the average distance per hunt. Luckily the speed of the predator per hunt is very easy, since the food doesn’t try to escape. It’s just a constant we’ll apply for now that will be a trait of Modelus Specius (Swimming Speed), until we revisit swimming and hydrodynamics later. Let’s say his speed is 10cm/s, or 0.1m/s.

This gives us the following set of equations:

Distance per Hunt = (0.66 * Patch Length) * (1 - (4 * Predator Population Density * Prey Population Density)) - Predator Body Radius - Prey Body Radius
Time per Hunt = Distance per Hunt / Speed per Hunt

Time Spent Hunting

Now we must find the total time spent hunting every month. This value is PER INDIVIDUAL. Just because you have 2 lions doesn’t mean twice the time is spent hunting, because the lions will hunt simultaneously. So, we will calculate this next part by looking at the average individual member of Modelus Specius.

To find the total time spent hunting by the average individual, we just multiple the time per hunt by the number of hunts each individual needs to perform. Recall in the last part that we tracked the total amount of food consumed in the timestep. We are going to make a small tweak and change this into the food required, or in other words the hunts required. This represents the total number of hunts required by the population to feed themselves. This is important because now with movement speed, they may run out of time in the month to finish feeding!

If we divide the hunts required by the total population of predators we get the average number of prey/food that needs to be hunted by each predator, and since each hunt yields only 1 prey this also equals the number of hunts.

Hunts Required per Person = Hunts Required / Population
Required Hunting Time per Person = Hunts Required per Person * Time per Hunt

This gives us:

Distance per Hunt = (0.66 * Patch Length) * (1 - (4 * Predator Population Density * Prey Population Density)) - Predator Body Radius - Prey Body Radius
Time per Hunt = Distance per Hunt / Speed per Hunt
Hunts Required per Person = Hunts Required / Population
Required Hunting Time per Person = Hunts Required per Person * Time per Hunt

Successful Hunts

Remember that each timestep is 1 month. So we cap the maximum free time that an individual can spend hunting to 1 month. This means that if they require more than that, too bad, your time’s up. Think of it this way: If Jack needs to hunt 4 rabbits and he has 30 days to do it, but it takes 15 days to hunt each rabbit, sorry Jack you only get 2 rabbits.

Successful Hunts = Available Hunting Time per Person / Time per Hunt
Remaining Time = Free Time - Available Hunting Time per Person

This is a case that will be very unlikely to occur in our current simplified model though. It will become a more relevant concept as things get more complex.

Reproducing Time

Remember, we are tracking free time on the individual basis. So after the average individual finishes hunting, all the remaining time is used for reproduction. This gives us:

Reproducing Time per Person = Remaining Time

Which means we now tweak the births equation. Remember mating frequency gives the maximum births per month if you spend all month reproducing, but it has to be scaled down by how much time you can actually spend reproducing:

Births = Population * Available Reproducers * Mating Frequency * Reproducing Time per Person * Litter Size

Updating the Algorithm

At this point, the list of equations is growing long enough that I don’t think it’d be that helpful for me to just throw them all at you at the end of the part. If you really want it I can post it though. I’m also not really feeling the usefulness of the flow diagram. If someone wants it I can make it but otherwise I’ll ignore it for now.

Demo

However, the introduction of movement has now made the demo simulations a lot more interesting. Here is one using the conditions we discussed in this part. Note that some of these use different units in the calculations (the calculations use joules for example @hhyyrylainen ), but I’ve written them out here in easily understandable units.

Starting Conditions

• Simulation Time = 24 months
• Modelus Specius
  • Starting Population = 100
  • Available Reproducers = 1.0
  • Mating Frequency = 1/month
  • Litter Size = 1
  • Lifespan = 3 months
  • Base Metabolism = 300 calories/month
  • Swim Speed = 1cm/s
  • Body Radius = 0.5cm
  • Body Volume = 0.52cm^3
• Food
  • Starting Amount = 50000
  • Energy Yield = 1 calories
  • Regeneration Rate = 50000/month
  • Body Radius = 5cm
  • Body Volume = 523.6cm^3

There are a few cool takeaways from the data. We can see that the population grows rapidly at first since food is in abundance, and then stabilizes at a lower level when shortages hit. We can also see that they are able to finish hunting so quickly that every month they still spend over 90% of their time reproducing. At first, they spend about 7% of their time hunting, but as their population increases the average distance to the food goes down and so they cut down to only spending 3% of their time hunting by the end. Also the species density is not actually 0%, it’s just a very small number that doesn’t show up. I will do a follow-up post to this one where I’ll explore different starting conditions and see what outcomes we get to better explore the simulation we’ve got going so far.

---

Summary

New Performance Stats
Population Density
Required Hunts
Successful Hunts
Distance per Hunt
Time per Hunt
Hunting Time per Person
Reproducing Time per Person

New Traits
Swimming Speed
Body Radius
Body Volume

Topics for Discussion

• Can the mean distance between two points in a unit cube being 0.66 be scaled with the size of the cube?
• How do we want to approximate a patch to be shaped as? A cube? A sphere?
• In microbial gameplay, will we simulate patches as 2D?
• Comments and feedback are welcome!

[tjwhale]

Hi Nick, this is interesting to read. A few thoughts, sorry this came out really long unintentionally.

I really like the idea of breaking things down into Life Activities, that makes a lot of sense for working out how one change might impact a creature in different ways (like more armour improving combat but slowing grazing or something).

On the question of continuous Differential Equations and using tools from calculus vs Difference Equations (having discrete update steps as you are talking about) is that in terms of complexity they are much the same. Whenever you computer model a continuous Differential Equation you have to discretise first and then work with the corresponding Difference Equation. So the latter aren’t really any less complicated (though going with discrete time steps is the best way to go for us I agree),

In general with both these types of equations there is a tradeoff between complexity (and therefore accurately modelling the world if that is what you are trying to do) and analysis (being able to understand what the model will do) and control (being able to change the parameters of the model so that it gives you the behaviour you want). The more complex things become the harder it is to understand what is happening and the harder it is to control it.

Ultimately the thing we are giving the player is a control problem, which is: by changing your species blueprint (and other parameters like behaviour) can you get your population to a high level relative to the other species.

So if we use a highly complex model then the issue is that it will have chaotic dynamics and the player won’t be able to control it very easily. If you look at the Lotka-Volterra equations which are a very simple predator prey model you can see (just from looking at the graphs) that there are oscillations in the solutions. The model doesn’t converge to an equilibrium, it keeps changing over time.

This makes control quite a difficult problem. For example I could say “your pop is 25” which is the high point of a cycle and then you make some positive change to your creature and I say “your pop is now 13” which is the low point of a cycle, so you undo the change and I tell you “your pop is now 18” which then feels like it makes no sense and so you do no changes and I say “your pop is now 23”. It feels very random.

You can do things like averaging but once the dynamics become sufficiently chaotic that won’t help as there will be oscillations of many different frequencies.

In general your model has been mostly linear (which will converge to a stable equilibrium) however when you introduce this “Predator Population Density * Prey Population Density” you are introducing a non-linearity, which is going to start to lead you down the road to complicated, non-linear dynamics such as oscillations and chaos (which is in itself a really cool subject and a great thing to explore). Basically when prey is high predators will surge but then there will be too many predators so prey will collapse causing predators to collapse causing prey to surge etc.

So if you’d like to carry on with what you are doing feel free, I just kind of wanted to offer that as a warning that my guess about what will happen is as you introduce more non-linearities you will get more and more complex dynamics come out and it will become uncontrollable. However it might be a great learning experience to try it out for yourself and see what happens as you go further. I may also be completely wrong (that happens a lot) though differential equations was the subject of my PhD so I know something about them.

My most recent attempt at an auto-evo algorithm is here the basic idea is to have just an energy balance model. So for what you are doing it would be a bit like cutting everything out except just computing “at what level of population does food consumption = food generation or production” as that’s generally the equilibrium you are aiming for anyway.

The reason I think this might work well is it’s much more controllable, for example if you add another chloroplast then you get a little more light energy compared with the other species and that increases your population, if you take it off (and all other species stay the same) then the populations will all revert to what they were before you put it on, which makes it possible for the player to feel like they are controlling what is happening.

On top of this it will react to the patch conditions (which I think is the main goal), so patches with no sunlight will lose all their chloroplasts.

I am very open to further discussions and changes / switching to a new algorithm / merging ideas or anything really. Making the auto-evo system is really hard because firstly it’s a hard problem and secondly it’s very core to everyone’s expectations of how the game will work so there are a lot of different opinions from a lot of directions on whatever is produced (which is good I guess, it’s nice people care about the game )

And yeah don’t let me put you off, I am enjoying reading what you are doing so if you continue to write it I’ll continue to read.

[NickTheNick]

Everything about the balance of complexity, analysis, and control is very true, and something I thought about a lot going into starting this series. Ultimately I decided for it and these were the reasons I came up with:

• I’m already starting to see some oscillations reminiscent of Lotka-Volterra interactions with different starting conditions for part 3. The oscillations always stabilize around a mean though. However if future additions causes them to no longer do so, as long as the oscillations are regular enough around a certain mean I’d suggest we take that mean as the final value for the population. If we make changes and it produces oscillations AND they are chaotic (or even getting increasingly chaotic every round) I think that’s a point we need to step in as designers and change the implementation of that part to ensure we build a system that can be understood.
• In terms of analysis, I think it’s very important that the player understand enough but not all of what’s happening. By this I mean they should understand enough to be able to make smart decisions, but not enough that they can see through the entire apparatus and perfectly predict the best moves to make every time. It should be like chess, where there are many different options and the struggle IS to be able to think ahead and predict outcomes and plan responses.
• Expanding on the above point, I agree that it can easily become difficult to analyze the impact of your changes to the algorithm, UNLESS you track many of the stats and values over time and display them to the player. Even now in just part 3, it can be hard to predict what or why things are happening if you just look at months and population, but with all the other data available it allows you to see for example that the food ran out, or that the species has to spend most of its time hunting and thus doesn’t have much time left to reproduce, or patterns like that. If we reach a point where there’s simply too much information to display to the player without overwhelming them, I think that’s another point where we as designers need to intervene and simplify the model.
• In regards to the energy balance model you’ve made, I do like the approach and I think it greatly avoids the risk of chaos or lack of control, but from my understanding of it it lacks the depth or complexity I believe the auto-evo system should have. As the fundamental selling point of the first half of the game, I think the evolution system should be as detailed as we can make it within the bounds of balance and fun. Some recent games I have played have showed me that it definitely is possible to do this and still create a great game, such as Kerbal Space Program for rocket science, or Ymir for economics and city-building. I think the best part of creating a detailed system is that it creates a simulation, which can then produce realistic but new and unexpected outcomes which can surprise you on every playthrough (which I’m already starting to see a little bit of just at part 3), and produce more interesting interactions between its actors.
• Worst case scenario, it’s much easier to take a system that is too complex and simplify it, than to take a simple model and make it deeper and more complex. In fact many of the upcoming parts are far less groundbreaking than what we’ve implemented so far. For example food turned this from an exponential growth model into something that stabilizes, and movement introduces the oscillating effect of different species densities as you pointed out. This early stage is similar to building the framework and foundation of the house. However many future parts will just be filling in the rooms of the house, and not increase the complexity too much. We’ve got a part coming up on hydrodynamics, which acts to ultimately limit the swimming speed of species, and then the part on perception ultimately just reduces the number of predator-prey interactions, since they won’t always know where the prey are.
• Finally, even if we ultimately reject this approach and choose a different algorithm, I think it can teach us a lot about how to implement different features like swimming, population density, hunting, and more, and I do personally enjoy making the episodes and being able to play with the simulation.

[tjwhale]

I am very inspired by KSP too, that’s what I would like to push towards, a lego like set of building tools which the player uses to overcome complex and challenging scientific problems in a fun way.

@NickTheNick

Worst case scenario, it’s much easier to take a system that is too complex and simplify it, than to take a simple model and make it deeper and more complex.

I am not sure about this, I think the opposite might be true. However as with many things doing a bunch of experiments is a good way of proceeding.

Also on the issue of complexity I think it shouldn’t be so hard to find enough. Even simple games like the prisoners dilemma become complex and interesting when played iteratively between multiple agents with different strategies.

@NickTheNick

I do personally enjoy making the episodes and being able to play with the simulation.

Awesome

[NickTheNick]

Yeah I think experimentation is our major benefit. Since we are building it iteratively and from such a simple original framework, we can keep track of the entire algorithm as we build it and intervene if it starts to get too chaotic or complex at any point.

[NickTheNick]

Part 3.1: Simulation Demos

As I mentioned in the last part, we’ll now do a series of demos with different parameters to better explore the system we’ve created so far, and see how changes to traits affect the population of the species. Hopefully it can also give us a taste for what the finished Auto-Evo system will feel like in the game!

Before we begin, however, running these simulations was helpful since it helped me find to flaws with the algorithm’s design. Firstly, I realized that people should die of old age at the end of the timestep, not the beginning. If the lifespan for a species is 1 month or lower, the entire population will die of old age before they get to do anything, which doesn’t make any sense. This change doesn’t change anything other than fixing that problem, and I’m not really sure why I didn’t think of this earlier. Here is what the new Life Cycle Diagram looks like:

Which much more closely resembles the typical lifespan of an organism (birth, survival, reproduction, death from old age).

Secondly, I’ve renamed the Population Density performance stat to now be called Spatial Population Density, since it’s actually a measure of what ratio of space the population occupies. This is so that Population Density can refer to its actual meaning of a number of individuals per unit of area or unit of volume.

Finally, to make things more interesting, I’ve tweaked some of the stats of the Standard Simulation to make life more difficult for the species. Then the following changes will almost be an experiment to see which is the best mutation. In fact we’re basically playing as the Auto-Evo system here, since the system will assign random mutations to a species and see which one best increases its survival. First, let’s begin with our baseline, the Standard Simulation.

Simulation 0: Standard Simulation

Starting Conditions

• Simulation Time = 24 months
• Modelus Specius
  • Starting Population = 100
  • Available Reproducers = 1.0
  • Mating Frequency = 1/month
  • Litter Size = 1
  • Lifespan = 3 month
  • Base Metabolism = 300 calories/month
  • Swim Speed = 1cm/s
  • Body Radius = 0.5cm
  • Body Volume = 0.52cm^3
• Food
  • Starting Amount = 50000
  • Energy Yield = 1 calories
  • Regeneration Rate = 50000/month
  • Body Radius = 5cm
  • Body Volume = 523.6cm^3

In the original scenario, the population stabilizes at 270 individuals. We’ve analyzed why it follows the pattern we see in the past part, but to recap: The population grows quickly at first due to an abundance of food, but then when shortage hits it stabilizes at a lower level where the rates of food consumption match the rate of food regeneration.

Simulation 1: Increased Mating Frequency

Starting Conditions

• Simulation Time = 24 months
• Modelus Specius
  • Starting Population = 100
  • Available Reproducers = 1.0
  • Mating Frequency = 4/month
  • Litter Size = 1
  • Lifespan = 3 month
  • Base Metabolism = 300 calories/month
  • Swim Speed = 1cm/s
  • Body Radius = 0.5cm
  • Body Volume = 0.52cm^3
• Food
  • Starting Amount = 50000
  • Energy Yield = 1 calories
  • Regeneration Rate = 50000/month
  • Body Radius = 5cm
  • Body Volume = 523.6cm^3

The cells of Modelus Specius have evolved special proteins that greatly accelerate the replicating process, causing the cells to double their original number 4x as quickly as before to produce offspring organisms through budding.

In this scenario the population stabilizes at 767. It’s interesting to consider why an increase in mating frequency led to such an increase in population. It also seems like Modelus Specius spends less time of the month hunting. I think the main reason why we see the increase in population is that increased mating frequency means more births to offset the number of deaths from old age and starvation. In fact you can see that every year the majority of the population dies of starvation (600 of the 767), but the surviving 167 have so many offspring that it keeps the species alive. This is a very interesting strategy that I had never even considered so far, and keep in mind how simple our model currently is! It’s crazy to see how it can already start producing these interesting interactions.

Simulation 2: Increased Litter Size

Starting Conditions

• Simulation Time = 24 months
• Modelus Specius
  • Starting Population = 100
  • Available Reproducers = 1.0
  • Mating Frequency = 1/month
  • Litter Size = 4
  • Lifespan = 3 month
  • Base Metabolism = 300 calories/month
  • Swim Speed = 1cm/s
  • Body Radius = 0.5cm
  • Body Volume = 0.52cm^3
• Food
  • Starting Amount = 50000
  • Energy Yield = 1 calories
  • Regeneration Rate = 50000/month
  • Body Radius = 5cm
  • Body Volume = 523.6cm^3

A mutation to the DNA for Modelus Specius’ budding has created the unique situation where it grows four buds simultaneously and then releases all of them, increasing the number of offspring produced per reproduction.

I ran the numbers on this and it produces the exact same outcome as the scenario above. At the moment litter size and mating frequency have effectively the same effect on the simulation.

Simulation 3: Lower Base Metabolism

Starting Conditions

• Simulation Time = 24 months
• Modelus Specius
  • Starting Population = 100
  • Available Reproducers = 1.0
  • Mating Frequency = 1/month
  • Litter Size = 1
  • Lifespan = 3 month
  • Base Metabolism = 150 calories/month
  • Swim Speed = 1cm/s
  • Body Radius = 0.5cm
  • Body Volume = 0.52cm^3
• Food
  • Starting Amount = 50000
  • Energy Yield = 1 calories
  • Regeneration Rate = 50000/month
  • Body Radius = 5cm
  • Body Volume = 523.6cm^3

The cells of Modelus Specius have evolved a more efficient method of spending energy to perform processes in the body, and as such only require half as much energy (5 calories per individual per day) for their base metabolism.

In this scenario the population stabilizes at 548. Since the population consumes less energy at the start, it takes longer for the food shortage to hit so we see the population peak on the 5th month instead of the 2nd. My guess for the increase in population over the standard simulation is that since each individual only requires half as much energy, they only spend half as long hunting (2% of their time instead of 4%) which means they can spend that extra 2% of their time reproducing. It ALSO is because of the fact that with half the base metabolism as before, the environment now produces enough energy to support double the population.

Simulation 4: Increased Swim Speed

Starting Conditions

• Simulation Time = 24 months
• Modelus Specius
  • Starting Population = 100
  • Available Reproducers = 1.0
  • Mating Frequency = 1/month
  • Litter Size = 1
  • Lifespan = 3 month
  • Base Metabolism = 300 calories/month
  • Swim Speed = 10cm/s
  • Body Radius = 0.5cm
  • Body Volume = 0.52cm^3
• Food
  • Starting Amount = 50000
  • Energy Yield = 1 calories
  • Regeneration Rate = 50000/month
  • Body Radius = 5cm
  • Body Volume = 523.6cm^3

Some cells on the edges of Modelus Specius have evolved some of their internal proteins into elastic fibres that can cause them to expand and contract at a greater range of motion. This allows the organism to undulate with wider motions and swim faster (from 1cm/s to 10cm/s).

In this scenario the population stabilizes at 277 (remember standard simulation was 270). I think this tiny increase is because so little time was being spent hunting anyways, that increasing speed by 10x barely affects the overall population. Yes in the last simulation the less time spent hunting increased population, but remember it also involved less energy being consumed overall which greatly increased the OVERALL population that could be supported. Here the population cannot grow any larger because starvation rates will keep it in check.

Simulation 5: Higher Food Energy Yield

Starting Conditions

• Simulation Time = 24 months
• Modelus Specius
  • Starting Population = 100
  • Available Reproducers = 1.0
  • Mating Frequency = 1/month
  • Litter Size = 1
  • Lifespan = 3 month
  • Base Metabolism = 300 calories/month
  • Swim Speed = 1cm/s
  • Body Radius = 0.5cm
  • Body Volume = 0.52cm^3
• Food
  • Starting Amount = 50000
  • Energy Yield = 10 calories
  • Regeneration Rate = 50000/month
  • Body Radius = 5cm
  • Body Volume = 523.6cm^3

Chemical changes on the surface of the ocean have led to denser clouds of glucose floating in the oceans, containing 10x as much energy.

In this scenario, the population stabilizes at 2777. I know that this is technically not a mutation to the species but a change to the environment, but I wanted to try it too. We can see that increasing the energy yield of the food drastically affects the species’ population. It takes much longer for the food shortage to hit, so the population peaks on the 9th month instead of the 2nd. Also, each food cloud is so energy rich that each individual only needs to hunt 1 to receive all the energy they need for an entire month, drastically reducing the time they spend hunting. Since 50,000 units of food are produced every month, but the energy of that food has increased 10x, the environment can now support a much higher population with the energy it produces. For all these reasons (and maybe a few more I’m not thinking of), the population of Modelus Specius is effectively able to increase by 10x.

Final Results

Now we can look at the final population achieved with each mutation.

Obviously the Increased Food Energy Yield had the greatest effect, but let’s pretend we are Auto-Evo and that is not an option. We would choose Increased Mating Frequency or Increased Litter Size as the mutation for Modelus Specius, since it produced the greatest increase in population size.

Also keep in mind that the “strength” of those different mutations depended a lot on the conditions of the environment. Since energy was so abundant, lower base metabolism and increased swim speed were not as effective as adaptations, whereas increased mating frequency or increased litter size allowed the species to rapidly grow its population and make greater use of the plentitude of energy in the environment. Perhaps if energy was much harder to come by, lower base metabolism and increased swim speed would have been much better adaptations!

I hope you guys found that interesting and that it helped give a sense of how the algorithm works and how it will ultimately be used to guide Auto-Evo. It definitely did whet my appetite for seeing evolution in action in the final game. I think these demo simulations will only get more and more interesting as we add more elements to the algorithm. Next time we’ll be back with the next part in the series!

[NickTheNick]

FOREWORD
After some thought and discussions on Discord, I’ve realized that this next part is actually mostly unnecessary. However, it’s worth discussing the parts of it that matter, so get ready for probably the shortest part of this series.

Part 4: Demography

As you can see, within just a few parts we’ve already quite rapidly created a rudimentary auto-evo algorithm, with traits like swimming speed, base metabolism, and mating frequency factoring into the survivability of species. I really like the approach we are taking because it feels like we are building the framework of the algorithm, and then filling in the details later. We will soon be ready to start introducing other species into the mix, but before we can do that there are two quick topics we must cover in their own parts.

The first is this part, on habitats and demography. How does where the species live affect its likelihood of interactions with other species? We have already factored in density, but there’s also other factors of the distribution of species in nature such as preferred habitats, habitat overlap, clustering, etc.

We will revisit other aspects of habitats again in the future, such as migrations, environmental conditions, territoriality, etc. For now though, we must simply consider where in the patch Modelus Specius is likely to live and how that affects its interactions with other actors in the patch.

We will be breaking down the following 2 assumptions from our list:

• Modelus Specius is a flat, tiny, simple, jelly-like organism that lives at the bottom of the ocean.
• Members of the species can instantly perceive food regardless of distance (Perception)
• Members of the species can completely consume the food and gain 100% of the energy. (Hunting/Metabolism)
• The species is equally distributed/dispersed across the world (Demographics)
• The planet is one giant ocean of equal pressure water that is equally accessible to the player (Geography/Terrain)
• Modelus Specius is the only species on the planet (Ecology)
• Members can reproduce as many times as they want, instantly, with no pregnancy/gestation period. (Reproduction)
• The species reproduces via asexual reproduction, spawning fully developed offspring that can themselves immediately begin reproducing. (Mating)
• The species does not change in physiology as they age (Aging/Ontogeny)
• The species is fully aquatic (Terrestriality)
• Members of the species are solitary and do not cooperate with other species members in any way. (Cooperation/Sociality)
• The species has no parental instincts, and will immediately abandon offspring (Parenting)
• The species is perfectly adapted to its environment and suffers no death or disease from environmental conditions (Environment)

Questions to Consider

When addressing these two assumptions, there are a few questions that are raised:

• What would a species’ habitat look like? Can it be assumed that a species occupies the whole patch? Or only parts of the patch?
• If they only occupy parts of the patch, how do we calculate overlap?
• Is the species evenly distributed across the entire habitat they occupy? Or are they clustered?
• Are there inaccessible zones of the patch? (Physical barriers, isolated bodies of water, pressure differences, other physiochemical differences)

Habitats

What would a species’ habitat look like? Can it be assumed that a species occupies the whole patch? Or only parts of the patch?

From the definition of a patch, we are going to assume that all species in a patch occupy all parts of that patch. Habitats thus will not be defined by what parts inside of a patch are occupied by the species, but rather which specific patches are occupied in the first place. For example, consider the following diagram:

A species of camels would have their habitat defined by the 8 Desert patches that they occupy. However, within those patches the camels would be assumed to live in the entire area/space. This concept will be explored more in Episode 2.

Patches will tend to be smaller and represent a piece of land or ocean or sky that has very similar living conditions all across, so this is a fair assumption to make.

Overlap

If they only occupy parts of the patch, how do we calculate overlap?

This question is irrelevant because of the answer to the first question. Since we are not assigning specific habitats inside of a patch, overlap is unnecessary because all species in a patch will ALWAYS overlap. Therefore overlap will be more in regards to whether 2 species live in the same patch, and how many patches they live together in. This is something to revisit in Episode 2.

Clustering

Is the species evenly distributed across the entire habitat they occupy? Or are they clustered?

Here is an interesting point to consider. It might be difficult to imagine how clustering would affect demographics, so here’s a diagram to help illustrate the point.

Imagine a scenario with multiple species that fill up the entire patch, aka a case of high spatial density (remember that population density was renamed to spatial density). With even distribution, as seen on the left side, the average distance between any one species and the nearest member of another species is quite short, something we explored in part 3. When distribution is even, this is equivalent to minimal clustering (or a clustering value of 0).

When clustering is maximized (a clustering value of 1.0), all species are lumped into big groups. Notice how suddenly the average distance between any species member and a member from another species becomes much longer. For example the orange species members are now much further from the red species members.

So imagine you are a predator. Increased spatial density of your species and the prey species is a BENEFIT because it makes it more likely for a prey to be very nearby to you. Therefore, increased clustering diminishes the benefit of spatial density by grouping members of a species together, instead of allowing them to be mixed in. Another way of thinking about it: Increased density decreases the average distance to a prey, and increased clustering decreases the effect of density, therefore increased clustering increases the average distance to a prey.

On the flip side, when spatial density is low, clustering doesn’t really matter because there are fewer individuals (think of just 1 predator and 1 prey, clustering is irrelevant in such a case because there is no one to cluster with).

So this is the current equation for calculating the average distance between a predator and its prey, factoring in the spatial density of both species:

Distance per Hunt = (0.66 * Patch Length) * (1 - (4 * Predator Population Density * Prey Population Density)) - Predator Body Radius - Prey Body Radius

Now we’ll add in a term that diminishes the density term. First we calculating the Average Clustering between the two species, and then factor that into the overall equation:

Average Clustering = (Predator Clustering + Prey Clustering) / 2
Distance per Hunt = (0.66 * Patch Length) * (1 - (4 * Predator Population Density * Prey Population Density * (1 - Average Clustering))) - Predator Body Radius - Prey Body Radius

With the above equation, when density is high then high clustering can reduce its effect, but when density is low the level of clustering is irrelevant. Clustering can never actually make the average distance to a prey increase more than it normally would be, it can only reduce density’s effect of making it shorter.

NOTE: Clustering will be defined as a species trait. Why would a species ever evolve clustering? If you are a prey to many species, it will make it less likely for you to be found by predators since you can hide all your species members in a corner. Also, clustering will be necessary for cooperative social behaviours that we’ll introduce in a future part.

Inaccessible Zones

Are there inaccessible zones of the patch? (Physical barriers, isolated bodies of water, pressure differences, other physiochemical differences)

To this I would again say no due to the definition of a patch. A patch is defined as a contiguous space with common physicochemical features, so if there was a barrier that would define a separate patch. Thus we don’t need to consider this.

Filling up the Oceans

Finally, before we can close, there’s one more point to consider. The algorithm actually currently has no limit on the number of organisms that can exist in the patch. Modelus Specius could theoretically have millions of offspring and fill the oceans of the world multiple times over (if there was enough food). We should introduce a limitation in terms of physical space to prevent this from ever occurring.

We will do this by limiting births. If the number of births is ever going to produce more offspring than can physically fit in the patch, we will just limit it to what can physically fit. I’ll skip showing the math behind this because I think it makes sense already, but if someone wants to see the equations for it let me know.

Demos

There will be no demos this part, since the changes were so minor and barely visible in the results. I did notice though that increasing clustering did lead to either more time spent hunting, or lower overall populations for Modelus Specius because of less free time to reproduce.

As compensation for this less eventful part, the next part will be coming out pretty soon!

---

Summary

New Performance Stats
None

New Traits
Clustering

Topics for Discussion
All comments and feedback are welcome!

[NickTheNick]

I realized I made a mistake with the corrected diagram at the top of this post. It should actually look like this:

In the updated algorithm, the first thing that happens is that the script determines what fraction of the population dies from starvation and kills them off first. Then of the remaining population, it determines how many offspring were birthed. Before it adds the births, it also kills off any of the population members who die from old age. Therefore births and old age deaths occur sort of in parallel.

Anyways, just wanted to make that clear and I’ll go back and fix the original post later. The next part will be coming up soon! Feel free to leave any suggestions or feedback you have on the series so far.

[NickTheNick]

Part 5: Hydrodynamics and Swimming

Yes we have a stat for movement speed now, but it’s a generic stat that is not tied to the organism’s body or the environment in any way. In this part we will look at the hydrodynamics of swimming and how to make movement speed realistically determined. There are no specific assumptions from our list that we are breaking down, instead we are just adding detail to the movement calculations from Part 3. Let’s find out how to make a creature’s swimming speed depend on its size, shape, and surroundings.

Undulation

Modelus Specius is a simple, spherical creature comprised of simple tissue. We’ll assume that this simple tissue has basic abilities to perform various tasks, such as in this case contracting to act like a muscle. We’ll classify Modelus Specius as using the type of swimming referred to as undulation, meaning it flexes the sides of its spherical body back and forth to propel itself forward. Thus we’ll say only the tissue on the sides of its body are contributing their force towards the swimming motion.

It’s hard to imagine how a solid sphere would use undulation, so imagine it as similar to the motion used by jellyfish (except that there is no hollow cavity or tentacles in the bottom).

Online, it says that the fastest recorded speed of a jellyfish is 8 kph. Dividing by ten I think gives us a more realistic top speed for small and simple jellies that are similar to Modelus Specius, so a top speed of 0.8 kph or 0.2 m/s. Now, for the next step, let’s take a look at Forces.

Force

Force is a simple concept in physics. It’s basically an interaction or energy that changes the motion of an object. When an object experiences a net force in a direction, it accelerates in that direction. When an object experiences no net forces in a direction, it maintains its motion in that direction (which could be maintaining its current speed without decelerating, or it could be being completely motionless). Keep in mind that accelerating in one direction (such as backwards) is the same as decelerating in the opposite direction (forwards). Why “net” force by the way? Because you can have multiple forces that act in opposing directions, but the ones that are greater will determine how the object’s motion changes.

For Modelus Specius’ swimming, we will consider its motion as an interplay of two forces: The “thrust” or “swim” force that the organism produces to propel itself forwards, and the drag force of water pushing back against it as it swims. We can visually display these using a diagram common in physics, a free-body diagram

Drag Force

At top speed, the swim force and the drag force will perfectly balance each other out, resulting in top speed being achieved and no more forward acceleration. Why is this the case? Because when you first start swimming, your Swim Force greatly outweighs your Drag Force. However, Drag Force increases with your speed, so as you speed up your Drag Force increased but your Swim Force stays the same. Eventually your Drag Forces reaches the value of your Swim Force, and that’s when you hit top speed and stop accelerating.

We already know the top speed of the Modelus Specius, which we’ve estimated at 0.2 m/s. But what if the ocean’s temperature changed and made water more resistant to swimming (higher drag)? What if Modelus Specius’ size got larger and less hydrodynamically shaped? Since drag force can vary so much, we should use our estimate of 0.2 m/s top speed to find the actual Swim Force produced by the jellyfish.

To find the Swim Force, we will find the Drag Force and know that by definition the Swim Force has to be the same value. Drag Force can be calculated using the following equation:

Let’s break this equation down variable by variable to see how drag will be calculated in Thrive.

Relative Flow Velocity

This refers to the difference of velocity (remember that velocity is just a physics term for speed with a direction) between the fluid and the object.

If the fluid flows in the opposite direction to the organism’s motion, then you add the velocities to find the relative velocity. If flowing in the same direction like the 2nd panel, you subtract them (if you and the water are both moving the same way, it feels like you’re not moving). If the water is motionless, you only consider the velocity of the organism. Okay, simple enough, but this brings us to a dilemma.

---

The Dilemma

Now obviously ocean currents are a very real phenomenon that play a big role in life, but I simply cannot imagine how to make an algorithm that takes into account the role of water currents, especially when most of the values being used are averages. Water currents flow in different directions at different speeds all over the ocean. Do we just take an average direction and average speed for the entire patch’s water current?

Okay, say we do that, how do we factor that into the algorithm? Do we apply that to the speed of the organism when he is hunting? How do we know when the water current is flowing in the same direction as the movement? In the opposite direction? How do we know when it’s flowing at a 30 degree angle from the organism’s motion. We could theoretically get an “average direction” for all hunts, but how would that be calculated? We’d have to get an average position for the predator population, and an average position for the prey population. And keeping track of the positions of objects in the patch opens a WHOLE new can of worms…

---

There are two possible solutions I see to this problem:

1. Completely ignore ocean currents and always assume the fluid’s velocity is 0.
2. Completely ignore ocean currents within a patch, but consider ocean currents between patches.

Ignoring Ocean Currents

This is a simple solution that makes it so that we always only consider the velocity of the organism.

Ocean Currents Between Patches

In this scenario, you do the same as in the first solution, but instead you track ocean currents between patches. This means that ocean currents can affect things like migrations between patches, or even moving to another patch to hunt (if that is intended to be possible), but not any interactions within a patch. I feel like this solution doesn’t sacrifice too much realism since ocean currents play a more important role on the larger scale (between patches) than the smaller scale (within patches).

For our purposes, we will proceed using the 2nd solution, which means the relative fluid velocity is equal to the velocity of the organism, which is 0.2 m/s. This gives us so far:

Drag Force = 0.2^2

Density of the Fluid

Next we must consider the density of the ocean. The density of ocean water on the surface is 1027 kg/m^3. As you go deeper, the density of seawater increases. However, it increases at different rates depending on what latitude you are at. Seawater at latitudes of around 30-40 degrees south (a region called the Pycnocline) follow this pattern:

Modelus Specius lives at the bottom of the ocean, so let’s say the depth of the patch is 4000m. Assuming similar conditions to Earth at 30-40 degrees south, this gives us a density of 1028 kg/m^3. This means drag force is now:

Drag Force = 1028 * 0.2^2

We can simplify this and divide it by 2 (to get rid of the fraction in the formula) to get:

Drag Force = 20.56

Reference Area

When you swim into a certain direction, even though you are a 3D shape you are presenting a 2D profile or “silhouette” to the water. This “side” or “face” depends on which side you swim with, aka where is your front. Since Modelus Specius is a sphere, the frontal surface area is just a circle. In fact for a sphere any direction you look at it its 2D profile is just an equally shaped circle. Using the radius of Modelus Specius which we earlier defined as 0.5 cm, that gives us a circle area of 0.000079‬ m^2. This gives us:

Drag Force = 20.56 * 0.000079<U+202C> = 0.0016

Drag Coefficient

The drag coefficient is a value that takes into account the shape and texture of the object for how much drag it experiences. Many tests have already been done to find the Drag Coefficients for many reference shapes:

The Organism Editor will look at any species and assign the nearest approximation of drag coefficient based on what shape the front-side is closest to. Evolutions to skin (like hydrodynamically shaped scales) can increase or reduce the drag coefficient. Since Modelus Specius is a solid sphere, we’ll use the drag coefficient of 0.47.

Drag Force = 0.0016 * 0.47 = 0.00076

And that’s it! Our Drag Force is 0.00076 Newtons (the unit for force, also shortened to N). This means Modelus Specius must generate 0.00076 N of Swim Force.

Swim Force

When a muscle flexes, it produces a certain amount of force based off of the cross-sectional area of the muscle. Therefore if you know the area of the muscle, and since we know the force produced per area, you know the force the whole area can produce. Well for Modelus Specius it’s backwards, since we know the total force it can produce, and the total area involved in undulation, we can work backwards to find the force produced per area.

An example of cross-sectional area of human muscles.

A total of 0.00076N of force is being produced to swim when at top speed. The cross-sectional area of Modelus Specius is 0.000079‬ m^2. However, for realism’s purposes I would say that perhaps only 50% of the cells in the sphere are flexing and unflexing to produce the swimming motion, so that means half of that area so 0.000039 m^2. This gives a force per area of 19.5 N/m^2. Human muscle has a force per area of 350000 N/m^2. Yes, a lot more, but humans have also had millions of years to evolve their muscles to become incredibly efficient, whereas Modelus Specius is a very primitive species with very simple muscle fiber cells.

Updating the Algorithm

So now we have some values that we can put into the algorithm. Muscle Area (the area of cells involved in undulation), and Muscle Strength (the Newtons produced per area of the muscle). An organism uses these to produce Swim Force. Swim Force is then compared to the Drag Force caused by the environment, and the result determines the top speed of the organism.

One assumption this is making is that the organism will accelerate so quickly to its top speed that we can just use the top speed for its hunting speed, and ignore the time spent accelerating. For now we will have to make this assumption for simplicity’s sake, but in the future we can revisit this to try to flesh it out.

Demo

Running the updated algorithm gives us results very similar to Parts 4 and 3:

Starting Conditions

• Simulation Time = 24 months
• Modelus Specius
  • Starting Population = 100
  • Available Reproducers = 1.0
  • Mating Frequency = 1/month
  • Litter Size = 1
  • Lifespan = 3 months
  • Base Metabolism = 300 calories/month
  • Clustering = 0
  • Locomotion = Undulation
    • Muscle Area = 0.000039 m^2
    • Muscle Strength = 19.5 N/m^2
    • Drag Coefficient = 0.47
    • Frontal Surface Area = 0.000079 m^2
    • Swim Speed = 20cm/s (Derived from above above traits)
  • Body Radius = 0.5cm
  • Body Volume = 0.52cm^3
• Food
  Starting Amount = 50000
  Energy Yield = 1 calories
  Regeneration Rate = 50000/month
  Body Radius = 5cm
  Body Volume = 523.6cm^3

The population stabilizes around 277. The reason not much changed is that many of the changes we’ve made were under the hood, supporting more advanced interactions with other species and the environment in future parts. For example, we can now make environmental changes to the density of the oceans, or evolutionary changes to Modelus Specius’ body, and it will change the speed of its swimming. Something that did change though is that the speed of Modelus Specius is now around 20cm/s instead of 1cm/s, which has reduced the time they spend hunting every month to even less (0.22%).

Glad to be done with this pretty technical and not very rewarding part. Next time, we will finally, finally add in the main ingredient of evolution that we all love… Other species!

---

Summary

New Performance Stats
None

New Traits
Locomotion Type
Muscle Area (Swimming)
Muscle Strength (Swimming)
Coefficient of Drag
Frontal Surface Area

Topics for Discussion

• How do we model ocean currents?

[NickTheNick]

FOREWORD:

The addition of new species warranted some big changes to the algorithm’s code. Not only does Auto-Evo now have to loop through several species to run calculations every month, it also introduces new “race” mechanics to see who gets food first. These new features were much more complicated than I originally anticipated, and I basically learned the hard way why it’s so important to organize your code. I had to do an overhaul of the code to make it cleaner and more organized to add in the new features. I also had to greatly increase how much data was being displayed in the final reports to make them show a lot more information and use them for bugfixing. This way we can see much more detail into what is happening month by month and use it to debug the algorithm whenever I make a mistake (which I made a lot of when implementing these new features). There may have to be a part or two after this for bugfixing of the script if I catch any more. Anyways, all the major bugs have hopefully been ironed out, so time to showcase the next part!

Part 6: Competition

So far in the series, we’ve created a single species that eats, swims, reproduces, and inhabits certain parts of the patch based off density and clustering. But that’s not how evolution works, with just a single species. Evolution pits multiple species against each other! I think it’s time to start adding in some competition!

In this part we will be removing the following assumption from our list of assumptions:

• Modelus Specius is a flat, tiny, simple, jelly-like organism that lives at the bottom of the ocean.
• Members of the species can instantly perceive food regardless of distance (Perception)
• Members of the species can completely consume the food and gain 100% of the energy. (Hunting/Metabolism)
• Modelus Specius is the only species on the planet (Ecology)
• Members can reproduce as many times as they want, instantly, with no pregnancy/gestation period. (Reproduction)
• The species reproduces via asexual reproduction, spawning fully developed offspring that can themselves immediately begin reproducing. (Mating)
• The species does not change in physiology as they age (Aging/Ontogeny)
• The species is fully aquatic (Terrestriality)
• Members of the species are solitary and do not cooperate with other species members in any way. (Cooperation/Sociality)
• The species has no parental instincts, and will immediately abandon offspring (Parenting)
• The species is perfectly adapted to its environment and suffers no death or disease from environmental conditions (Environment)

We will start by adding one additional species to the environment. This species will have the exact same stats as Modelus Specius and feed on the same floating clouds of glucose. At the moment this is effectively equivalent to doubling the starting population of Modelus Specius, since they are both evenly matched. However instead of reaching an equilibrium with all of the population being in Modelus Specius, it will evenly split between the two species. After updating the algorithm, we’ll differ the stats of Species B to see if the environment reaches an equilibrium between the two species.

Then, once we have ironed out all the features of having two unique species in the environment, we will add two more species, and they will be given unique stats as well. Our goal is to create a simple environment of different species, that will serve as the foundation for the work we do in the future parts.

Also before we start, I tweaked some of the numbers of Modelus Specius to produce some more realistic outcomes for some of the statistics. Now the fraction spent hunting every month usually comes out closer to 30% of the month rather than 0.7%.

Summary of the changes

• Mating frequency was reduced by 50%
• Lifespan was increased to 12 months
• Base Metabolism was increased to 100 calories a day
• Muscle Strength reduced to 2.5N/m^2 (making the typical speed 7cm/s)

New Definitions

One more thing before we start the algorithm, it’s important to clarify the meaning of some terms I’ve been throwing around lately. I’ll add all of these entries to the glossary:

1. Generation: A generation refers to a “turn” in the game. For example, when you start the game you are playing on the first generation of your species. After reproducing, entering the editor, and a timestep passing, you resume play in the 2nd generation. Technically, yes, you could say that there’s thousands of generations that would’ve occurred in the thousands of years that passed during the timestep, but for the game’s purposes we call the time after each editor session a new “generation”.
2. Timestep: The time between generations is called the timestep. When a player enters the editor, does his stuff, and then returns to the game, the game fast forwards thousands or millions of years to represent the evolution that took place. That’s called a timestep. Every time the player reproduces and enters the editor, another timestep passes. Timestep just refers to the time that passed.
3. Simulation Step: This simply refers to the unit of time for simulation for the population algorithm. At the moment, this is one month. This means that all the calculations are run over the course of a month, and then repeated for however many months that we want the simulation to go for.

If there are any questions or suggestions about these definitions let me know. Anyways, on to the calculations!

Order of Calculations

One point I’ve been bringing up a lot is that the order of calculations is very important… Well it’s time to bring it up again! We are now going to have several species running inside the simulation at once, so the order of calculation is critical for decisions such as who gets first access to food.

Turn Order

My original idea was to use a “Turn Order” to handle the multiple species. This is because of the way the algorithm is designed, where we calculate the population change of one species at a time over one month, and then repeat that however many months. At the end of a generation, the game would randomly pick a turn order for all the available species, and then every month it would run once through that list in the order they were assigned, running the population algorithm on each species. This meant that if a species was lucky enough to be at the top of the list, he’d feed first every month of a simulation before anyone else. This also meant that in times of shortage the bottom species on the list could get no food and immediately go extinct. I originally thought this was fair since it was random every time, so everyone had a chance of going extinct and on a future generation a different order of species could be picked, where perhaps you’re at the top. However, I realized that this was not allowing for the species to actually compete with each other in times of shortages.

Simultaneous Simulation

So instead, I decided to implement a simultaneous “race” whenever there is a shortage of food. In any month that there is more food than food that is hunted, the race mechanic is irrelevant and everyone gets the food they want. However, whenever there’s a shortage, the Success Rate of each species hunting the food determines what fraction of the food they get. For example, if Modelus Specius and the other specius combined want to hunt 10,000 food, but there’s only 1,000 food remaining, then if Modelus Specius has a success rate of 75% he gets 75% of the 1,000 and the other species gets the remaining 25%.

How do you calculate Success Rate you ask? Let me explain.

Race for the Food

Let’s first define the two species we have. We have Modelus Specius, the species one we know and love, and now we’ll introduce a second species called Propagatus Maxima. For now they will have the exact same stats. We’ll define a new statistic called Competitiveness, which will be used to calculate the success rate of each species in hunting the food.

Speed

We have no combat in our simulation at the moment, so competing for food is purely determined by who’s the fastest to get it first. We’ll represent this by having the species’ speed compared to the combined speed of all the other species. If Modelus and Propagatus have the exact same speed, say 1m/s, then each wins 50% of the contests. Here’s the mathematical form:

Success Rate = Speed of Modelus / ( Speed of Modelus + Speed of Propagatus)
Success Rate = 1 / (1+1) = 1 / 2 = 0.5 = 50%

However, if Modelus had twice the speed of Propagatus, he would win a larger share of the contests (in this case 2/3).

Success Rate = Speed of Modelus / ( Speed of Modelus + Speed of Propagatus)
Success Rate = 2 / (2+1) = 2 / 3 = 0.67 = 67%

So the greater your speed compared to the competition, the larger share of contests/races you win. Interestingly, with this equation no matter how fast your competitors are you’ll always get at least some of the food (representing hunts where you get lucky).

Population

Okay, but what if the slower species outnumbers the faster one 10:1? Shouldn’t that give a competitive advantage to the larger population since there’s more of them? Yes, so let’s introduce that into the mix.

Say cheetahs and hyenas both hunt antelopes. The cheetah can easily catch an antelope before a hyena 90% of the time because of his speed advantage. But, there’s only 1 cheetah whereas there are 100 hyenas. After that cheetah catches his first antelope, he doesn’t compete with the hyenas anymore and they’re free to now chase antelopes completely uncontested.

We’ll model this by having the Required Hunts of the species multiplied by its speed in the equation. If a species requires a lot of hunts, they’ll be competing for the prey a lot more and thus increasing their competitiveness. A species that is faster but requires less hunts will be like the cheetah and leave the competition early once they get their fill.

This does make a big assumption, and that is that there is no intraspecific competition (competition between members of the same species). I have avoided that so far since I cannot think of a good way to implement it, so please pitch in if you have any ideas on how to model it mathematically.

Say Modelus has twice the speed but Propagatus requires twice the hunts, this will look like:

Success Rate = (Speed of Modelus * Required Hunts for Modelus) / (Speed of Modelus * Required Hunts for Modelus + Speed of Propagatus * Required Hunts for Propagatus)
Success Rate = 2*100 / (2*100 + 1*200) = 200 / (200+200) = 200/400 = 0.50 = 50%

Their two advantages balance out and they both win half the contests. If one species had double the speed and double the required hunts, they’d win 80% of the contests (4x the success rate of their competitor).

Priority

One final component we are missing though. Two species could both have the same speed and same required hunts, but different Priorities for their prey. The cheetahs do all their hunting on antelopes, while the hyenas spend half their time hunting antelopes and the other half hunting zebras. Priority is a proportion simply representing what fraction of their energy they try to get from a given prey. This gives us the final form of the equation:

Success Rate = (Speed of Modelus * Required Hunts for Modelus * Modelus Priority for Food) / (Speed of Modelus * Required Hunts for Modelus * Modelus Priority for Food + Speed of Propagatus * Required Hunts for Propagatus * Propagatus Priority for Food)

Note that at the moment, there are only two species and they both chase after the same food, so they both have a priority of 1.00 for the food. In the future, we’ll create more complex food webs with predators having multiple different preys, so Modelus Specius could have for example a priority of 0.5 for Prey 1, 0.3 for Prey 2, and 0.2 for Prey 3 (all of a predator’s priorities must add up to 1.00).

To recap, we calculate the Competitiveness of a species for a given prey, and compare that to the Pooled Competitiveness of all predators hunting that prey. Using this equation, we can determine the success rate of two or more predators that hunt for the same prey based off their speed, required hunts, and prey priorities. In times of shortage, the success rate determines what fraction of the food they receive.

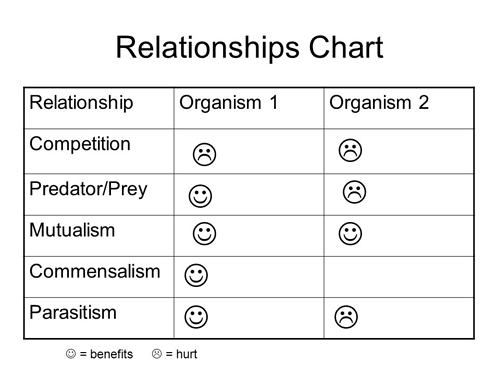
Competition is a Lose-Lose

If you have studied some biology you might know, competition is a lose-lose for both parties involved. Not only does competition harm you during times of shortage, but it also interferes in times of plenty as well.

We will get to the other interactions listed on that chart in future parts. For now we’ll discuss competition.

Assume that you are Modelus, and there is an equal population of Propagatus in your patch that is perfectly even in all stats. You both hunt for the same clouds of glucose. Statistically speaking, half the time you are likely to have a member of Propagatus beat you to the food you are chasing, and have to start a new chase. So even when food is in abundance the competition increases the time you need to spend on every hunt. We will also model this using Success Rate. If the two species are perfectly evenly matched in speed, required hunts, and prey priority, you will only have a Success Rate of 50%. If you are only winning 50% of the hunting contests, your average hunting time increases by 50%. This is because you need to hunt twice as much, since half your hunts are failing, to get the amount of food you need. If you are winning 90% of the hunts, then your average hunting time only increases by 10%. Recall the equation for Time per Hunt:

Time per Hunt = Distance per Hunt / Species Swim Speed

We’ll now update this to:

Time per Hunt = (Distance per Hunt / Species Swim Speed) * (1 / Hunting Success Rate)

NOTE: Hunting Success Rate is an average of the hunting success rates for all the preys that a species hunts. It is weighted by how many hunts are performed on that prey.

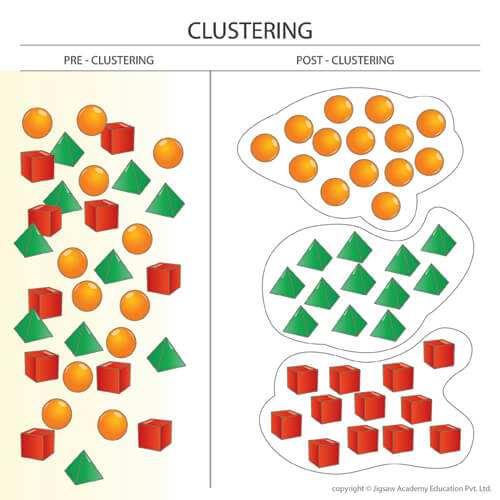
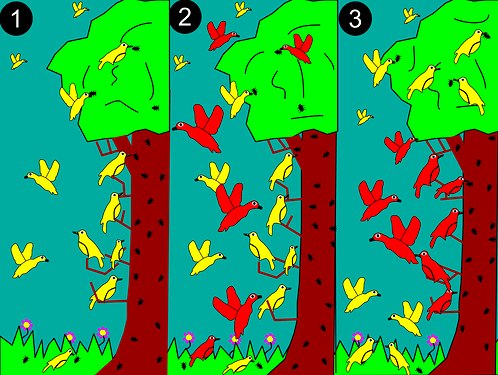
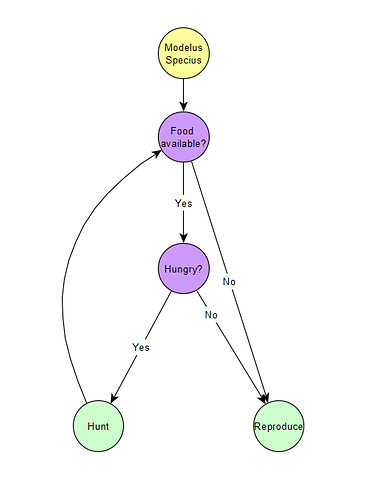
So we can see that even with ZERO shortage, competition increases the time spent hunting for all predators, even if any of the predators have an advantage. This should lead to a phenomenon observed in biology called the Competitive Exclusion Principle, which says that competition between multiple species for a single role will ALWAYS lead to one species winning and the others going extinct or evolving for different roles/niches. We will discuss this more when we run the demos.

The diagram above gives a simple illustration of the Principle.

And that’s all for the mathematical explanations of this part. Even though these explanations were shorter than previous parts, I probably spent 10x longer actually coding the prototype for this part, because of the complexity of the newly introduced interactions.

Demo with 2 Equal Species

Without further ado, let’s see how the introduction of new species changes the simulation! We currently have two species, Modelus Specius and Propagatus Maxima, and they have the exact same stats in all respects. Let’s see the starting conditions:

Simulation Conditions

Patch

Food

Modelus Specius

Propagatus Maxima

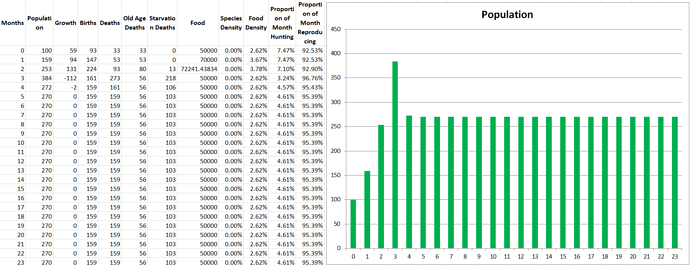
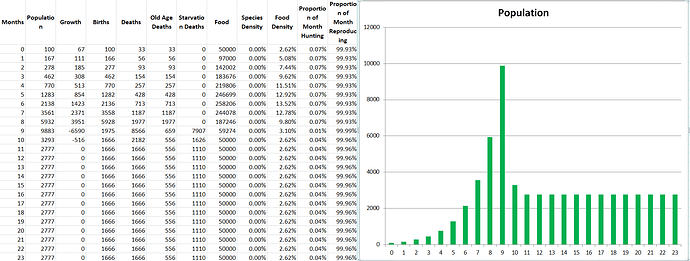
Running a demo of the two species produces the exact outcome we would expect, they perfectly match each other in population size the entire simulation, stabilizing at 446 members each. It’s not even necessary to show the graph for this demo, but at least we know the code is working as intended so far.

Demo with 2 Unique Species

Now for the one we were waiting for, where we assign different stats to each species. We’ll start by doing a very, very small change. We’ll simply increase the strength of Modelus Specius’ muscles from 2.5 N/m^2 to 3.5 N/m^2. A harmless evolution, right?

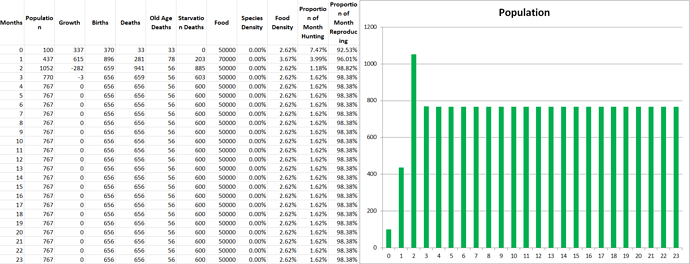
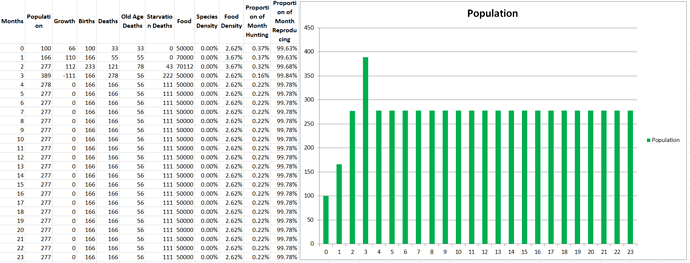
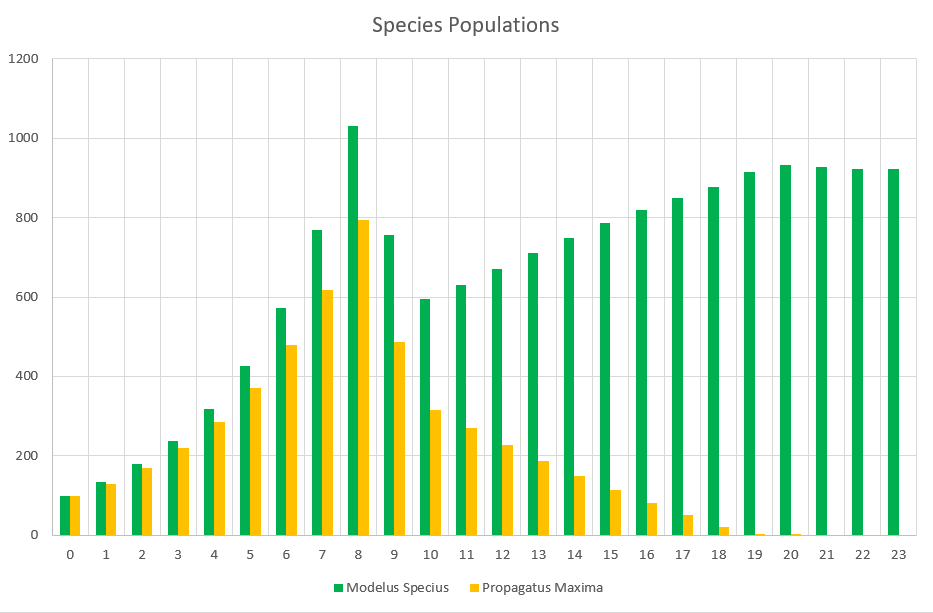
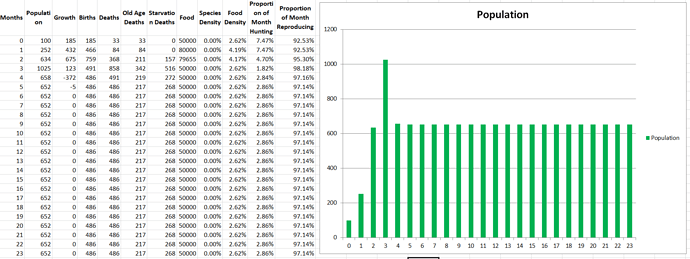
Propagatus Maxima went extinct in 21 months, while Modelus Specius survived and thrived and stabilized at 923 members.

So what’s the story. We can see the exponential growth at the beginning as there is an abundance of food. Notice that Modelus always seems to grow a little faster than Propagatus. Then the food shortage kicks in on the 8th month, and both populations lose a lot of members. However, Propagatus never recovers! Why is this? It’s because when there is an abundance of food competition increases the time spent to hunt but everyone gets all the food they need eventually (unless it takes them sooo long that they run out of time in the month). However, after the shortage starts, there is only so much food to go around every month. Modelus’ slight speed advantage lets them win more of the scarce food on month 9, which leads to a bigger gap between the two species’ populations by month 10. This bigger gap allows Modelus to win even more of the food, and the cycle continues until Propagatus goes extinct. What does this remind you of? That’s right, the Competitive Exclusion Principle. This is a perfect example of the principle in action, since both species are hunting the same “Food” which makes them competitors for the same niche.

A niche is akin to a “role” of a species in an ecosystem, defined by where it lives, what it hunts, and other such factors.

Interesting to note that even such a small competitive advantage of Modelus Specius over Propagatus Maxima builds up to a huge difference in population, and will eventually lead to Propagatus going extinct. This is exactly what is described by the Competitive Exclusion Principle, and it’s fascinating that this pattern emerged without us even specifically trying to put it into the algorithm. We simply modelled realistic interactions and have started to produce a realistic system! I have high hopes for where this algorithm can go!

Just a quick aside, now that we’ve got multiple species I’ll probably skip showing the tables with the monthly statistics since it would just be way too much information (since it’s one table for every species). I can keep posting them though if you guys really want them. For now though, I’ll show you Modelus’ report just so that we can understand what is happening:

What are some of the interesting patterns you see? Well for one thing you can see that the time per hunt goes down every month, and this is because Modelus is facing less and less competition as Propagatus dies off. This gradually leads to them having more free time to reproduce, which increases their birth rate and helps them reach a higher population.

One thing this demo has taught me though is that I feel that the starvation penalties may be a bit too harsh.

Less Severe Starvation Rules

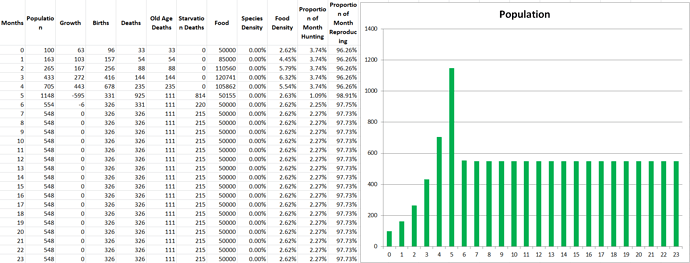
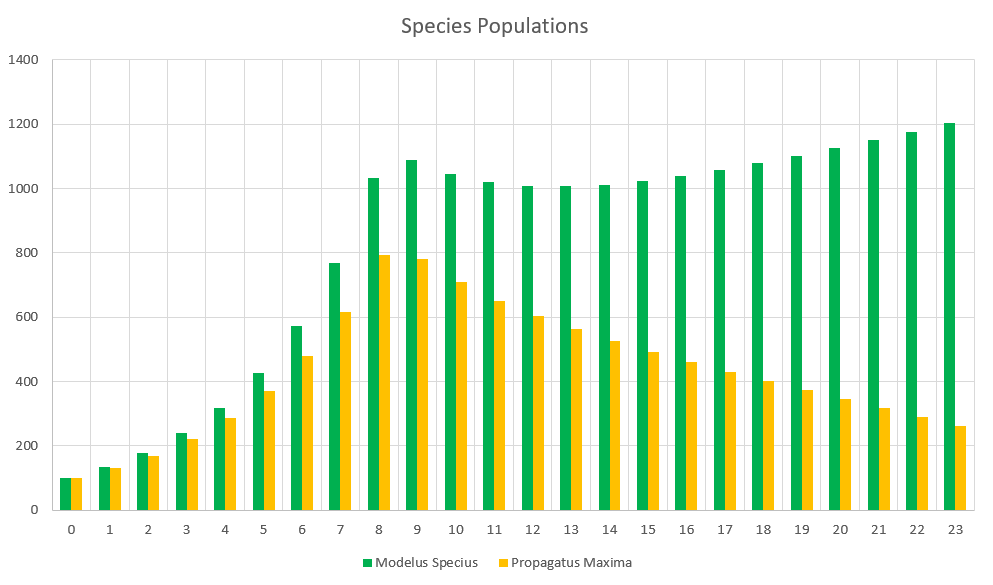
At the moment, 100% of the starving population of a species will die next month. This leads to very sudden extinctions when food runs out. I know that making this value any less than 100% seems very unrealistic since it seems like you’re saying species members can survive over a month without eating. To counter that, I’d say that this percentage can also represent how much energy ALL species members are receiving. 75% Proportion Fed could also mean that ALL species members only receive 75% of the energy they need. So to create a bit of a “softer landing” for species that run low on food, and not letting them go extinct extremely quickly, let’s try making it so that only 50% of starving species members will die. This means starvation is of course still bad but not the game-ending event it was before. This means that your species could technically eat 0 food for an entire month, and only 50% of them would die. Is that entirely realistic? I’m not sure, but we cannot make any more granular changes unless we make the timesteps smaller, and perhaps this is better for balance. Let’s see how this affects the simulation with the same conditions as before.

There we go, a much less severe drop for Propagatus. Even though he looks like he is still destined to go extinct under the current conditions, he at least won’t do so in under 2 years. We can play with the severity of starvation to get the results we like, so I’ll leave that open as a discussion question.

How severe should starvation be?

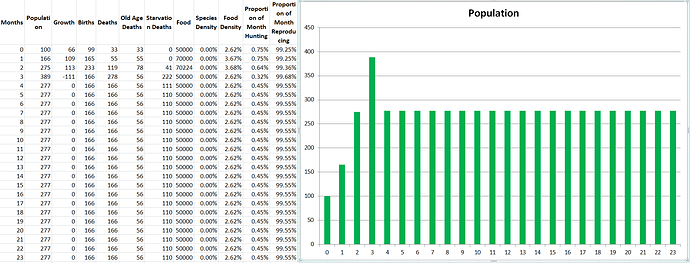
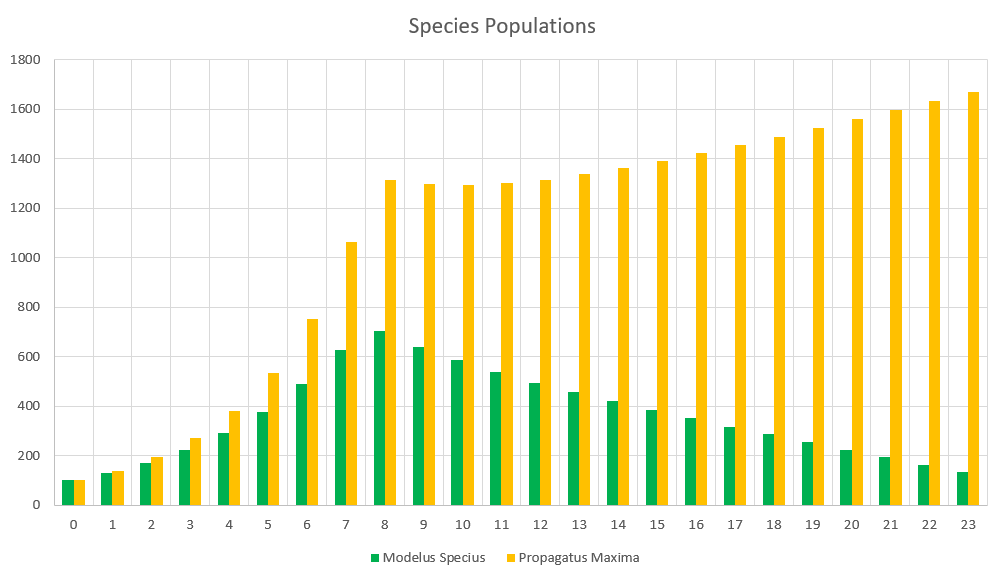
One more demo with 2 species. This time let’s make Propagatus Maxima into the species he was intended to be. Modelus Specius’ strength will be set back down to 2.5, but instead Propagatus will have 20% higher mating frequency than Modelus.

Holy cow. Clearly increasing mating frequency appears to still be very overpowered. We can revisit potentially balancing that in a future part.

This has been a lengthy post, but luckily with lots of cool new content! We are finally starting to see a lot more of the typical patterns we associate with evolution emerge in the system. I will do a sub-part soon where I’ll crank up the number of species in the simulation to 4, giving each of them unique advantages, and we’ll see who wins the game of evolution! Then after that, we’ll proceed with the next part of the series. Until then, please leave your feedback below!

---

Summary

New Performance Stats
Competitiveness
Pooled Competitiveness

New Traits
None

Topics for Discussion

• How do I model intra-specific competition (competition within a species)?
• Is it possible to make the time-steps smaller? This would allow for more realistic hunger/starvation modelling. Except this could also make the algorithm very computationally intensive.
• How severe should the consequences of starvation be? 100% death rate of all starving members?