FOREWORD:
The addition of new species warranted some big changes to the algorithm’s code. Not only does Auto-Evo now have to loop through several species to run calculations every month, it also introduces new “race” mechanics to see who gets food first. These new features were much more complicated than I originally anticipated, and I basically learned the hard way why it’s so important to organize your code. I had to do an overhaul of the code to make it cleaner and more organized to add in the new features. I also had to greatly increase how much data was being displayed in the final reports to make them show a lot more information and use them for bugfixing. This way we can see much more detail into what is happening month by month and use it to debug the algorithm whenever I make a mistake (which I made a lot of when implementing these new features). There may have to be a part or two after this for bugfixing of the script if I catch any more. Anyways, all the major bugs have hopefully been ironed out, so time to showcase the next part!
Part 6: Competition
So far in the series, we’ve created a single species that eats, swims, reproduces, and inhabits certain parts of the patch based off density and clustering. But that’s not how evolution works, with just a single species. Evolution pits multiple species against each other! I think it’s time to start adding in some competition!
In this part we will be removing the following assumption from our list of assumptions:
- Modelus Specius is a flat, tiny, simple, jelly-like organism that lives at the bottom of the ocean.
- Members of the species can instantly perceive food regardless of distance (Perception)
- Members of the species can completely consume the food and gain 100% of the energy. (Hunting/Metabolism)
- Modelus Specius is the only species on the planet (Ecology)
- Members can reproduce as many times as they want, instantly, with no pregnancy/gestation period. (Reproduction)
- The species reproduces via asexual reproduction, spawning fully developed offspring that can themselves immediately begin reproducing. (Mating)
- The species does not change in physiology as they age (Aging/Ontogeny)
- The species is fully aquatic (Terrestriality)
- Members of the species are solitary and do not cooperate with other species members in any way. (Cooperation/Sociality)
- The species has no parental instincts, and will immediately abandon offspring (Parenting)
- The species is perfectly adapted to its environment and suffers no death or disease from environmental conditions (Environment)
We will start by adding one additional species to the environment. This species will have the exact same stats as Modelus Specius and feed on the same floating clouds of glucose. At the moment this is effectively equivalent to doubling the starting population of Modelus Specius, since they are both evenly matched. However instead of reaching an equilibrium with all of the population being in Modelus Specius, it will evenly split between the two species. After updating the algorithm, we’ll differ the stats of Species B to see if the environment reaches an equilibrium between the two species.
Then, once we have ironed out all the features of having two unique species in the environment, we will add two more species, and they will be given unique stats as well. Our goal is to create a simple environment of different species, that will serve as the foundation for the work we do in the future parts.
Also before we start, I tweaked some of the numbers of Modelus Specius to produce some more realistic outcomes for some of the statistics. Now the fraction spent hunting every month usually comes out closer to 30% of the month rather than 0.7%.
Summary of the changes
- Mating frequency was reduced by 50%
- Lifespan was increased to 12 months
- Base Metabolism was increased to 100 calories a day
- Muscle Strength reduced to 2.5N/m^2 (making the typical speed 7cm/s)
New Definitions
One more thing before we start the algorithm, it’s important to clarify the meaning of some terms I’ve been throwing around lately. I’ll add all of these entries to the glossary:
- Generation: A generation refers to a “turn” in the game. For example, when you start the game you are playing on the first generation of your species. After reproducing, entering the editor, and a timestep passing, you resume play in the 2nd generation. Technically, yes, you could say that there’s thousands of generations that would’ve occurred in the thousands of years that passed during the timestep, but for the game’s purposes we call the time after each editor session a new “generation”.
- Timestep: The time between generations is called the timestep. When a player enters the editor, does his stuff, and then returns to the game, the game fast forwards thousands or millions of years to represent the evolution that took place. That’s called a timestep. Every time the player reproduces and enters the editor, another timestep passes. Timestep just refers to the time that passed.
- Simulation Step: This simply refers to the unit of time for simulation for the population algorithm. At the moment, this is one month. This means that all the calculations are run over the course of a month, and then repeated for however many months that we want the simulation to go for.
If there are any questions or suggestions about these definitions let me know. Anyways, on to the calculations!
Order of Calculations
One point I’ve been bringing up a lot is that the order of calculations is very important… Well it’s time to bring it up again! We are now going to have several species running inside the simulation at once, so the order of calculation is critical for decisions such as who gets first access to food.
Turn Order
My original idea was to use a “Turn Order” to handle the multiple species. This is because of the way the algorithm is designed, where we calculate the population change of one species at a time over one month, and then repeat that however many months. At the end of a generation, the game would randomly pick a turn order for all the available species, and then every month it would run once through that list in the order they were assigned, running the population algorithm on each species. This meant that if a species was lucky enough to be at the top of the list, he’d feed first every month of a simulation before anyone else. This also meant that in times of shortage the bottom species on the list could get no food and immediately go extinct. I originally thought this was fair since it was random every time, so everyone had a chance of going extinct and on a future generation a different order of species could be picked, where perhaps you’re at the top. However, I realized that this was not allowing for the species to actually compete with each other in times of shortages.
Simultaneous Simulation
So instead, I decided to implement a simultaneous “race” whenever there is a shortage of food. In any month that there is more food than food that is hunted, the race mechanic is irrelevant and everyone gets the food they want. However, whenever there’s a shortage, the Success Rate of each species hunting the food determines what fraction of the food they get. For example, if Modelus Specius and the other specius combined want to hunt 10,000 food, but there’s only 1,000 food remaining, then if Modelus Specius has a success rate of 75% he gets 75% of the 1,000 and the other species gets the remaining 25%.
How do you calculate Success Rate you ask? Let me explain.
Race for the Food
Let’s first define the two species we have. We have Modelus Specius, the species one we know and love, and now we’ll introduce a second species called Propagatus Maxima. For now they will have the exact same stats. We’ll define a new statistic called Competitiveness, which will be used to calculate the success rate of each species in hunting the food.
Speed
We have no combat in our simulation at the moment, so competing for food is purely determined by who’s the fastest to get it first. We’ll represent this by having the species’ speed compared to the combined speed of all the other species. If Modelus and Propagatus have the exact same speed, say 1m/s, then each wins 50% of the contests. Here’s the mathematical form:
Success Rate = Speed of Modelus / ( Speed of Modelus + Speed of Propagatus)
Success Rate = 1 / (1+1) = 1 / 2 = 0.5 = 50%
However, if Modelus had twice the speed of Propagatus, he would win a larger share of the contests (in this case 2/3).
Success Rate = Speed of Modelus / ( Speed of Modelus + Speed of Propagatus)
Success Rate = 2 / (2+1) = 2 / 3 = 0.67 = 67%
So the greater your speed compared to the competition, the larger share of contests/races you win. Interestingly, with this equation no matter how fast your competitors are you’ll always get at least some of the food (representing hunts where you get lucky).
Population
Okay, but what if the slower species outnumbers the faster one 10:1? Shouldn’t that give a competitive advantage to the larger population since there’s more of them? Yes, so let’s introduce that into the mix.
Say cheetahs and hyenas both hunt antelopes. The cheetah can easily catch an antelope before a hyena 90% of the time because of his speed advantage. But, there’s only 1 cheetah whereas there are 100 hyenas. After that cheetah catches his first antelope, he doesn’t compete with the hyenas anymore and they’re free to now chase antelopes completely uncontested.
We’ll model this by having the Required Hunts of the species multiplied by its speed in the equation. If a species requires a lot of hunts, they’ll be competing for the prey a lot more and thus increasing their competitiveness. A species that is faster but requires less hunts will be like the cheetah and leave the competition early once they get their fill.
This does make a big assumption, and that is that there is no intraspecific competition (competition between members of the same species). I have avoided that so far since I cannot think of a good way to implement it, so please pitch in if you have any ideas on how to model it mathematically.
Say Modelus has twice the speed but Propagatus requires twice the hunts, this will look like:
Success Rate = (Speed of Modelus * Required Hunts for Modelus) / (Speed of Modelus * Required Hunts for Modelus + Speed of Propagatus * Required Hunts for Propagatus)
Success Rate = 2*100 / (2*100 + 1*200) = 200 / (200+200) = 200/400 = 0.50 = 50%
Their two advantages balance out and they both win half the contests. If one species had double the speed and double the required hunts, they’d win 80% of the contests (4x the success rate of their competitor).
Priority
One final component we are missing though. Two species could both have the same speed and same required hunts, but different Priorities for their prey. The cheetahs do all their hunting on antelopes, while the hyenas spend half their time hunting antelopes and the other half hunting zebras. Priority is a proportion simply representing what fraction of their energy they try to get from a given prey. This gives us the final form of the equation:
Success Rate = (Speed of Modelus * Required Hunts for Modelus * Modelus Priority for Food) / (Speed of Modelus * Required Hunts for Modelus * Modelus Priority for Food + Speed of Propagatus * Required Hunts for Propagatus * Propagatus Priority for Food)
Note that at the moment, there are only two species and they both chase after the same food, so they both have a priority of 1.00 for the food. In the future, we’ll create more complex food webs with predators having multiple different preys, so Modelus Specius could have for example a priority of 0.5 for Prey 1, 0.3 for Prey 2, and 0.2 for Prey 3 (all of a predator’s priorities must add up to 1.00).
To recap, we calculate the Competitiveness of a species for a given prey, and compare that to the Pooled Competitiveness of all predators hunting that prey. Using this equation, we can determine the success rate of two or more predators that hunt for the same prey based off their speed, required hunts, and prey priorities. In times of shortage, the success rate determines what fraction of the food they receive.
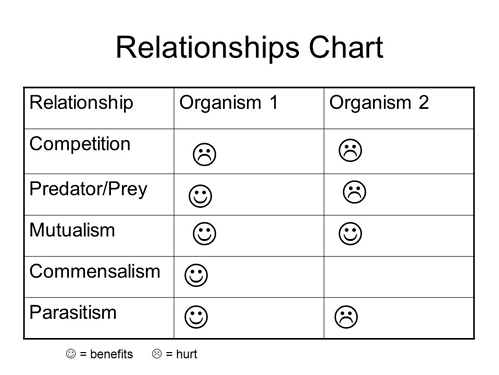
Competition is a Lose-Lose
If you have studied some biology you might know, competition is a lose-lose for both parties involved. Not only does competition harm you during times of shortage, but it also interferes in times of plenty as well.
We will get to the other interactions listed on that chart in future parts. For now we’ll discuss competition.
Assume that you are Modelus, and there is an equal population of Propagatus in your patch that is perfectly even in all stats. You both hunt for the same clouds of glucose. Statistically speaking, half the time you are likely to have a member of Propagatus beat you to the food you are chasing, and have to start a new chase. So even when food is in abundance the competition increases the time you need to spend on every hunt. We will also model this using Success Rate. If the two species are perfectly evenly matched in speed, required hunts, and prey priority, you will only have a Success Rate of 50%. If you are only winning 50% of the hunting contests, your average hunting time increases by 50%. This is because you need to hunt twice as much, since half your hunts are failing, to get the amount of food you need. If you are winning 90% of the hunts, then your average hunting time only increases by 10%. Recall the equation for Time per Hunt:
Time per Hunt = Distance per Hunt / Species Swim Speed
We’ll now update this to:
Time per Hunt = (Distance per Hunt / Species Swim Speed) * (1 / Hunting Success Rate)
NOTE: Hunting Success Rate is an average of the hunting success rates for all the preys that a species hunts. It is weighted by how many hunts are performed on that prey.
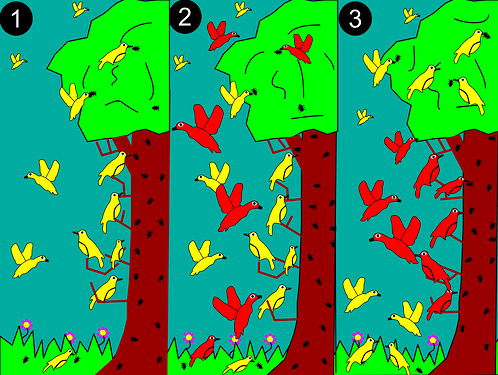
So we can see that even with ZERO shortage, competition increases the time spent hunting for all predators, even if any of the predators have an advantage. This should lead to a phenomenon observed in biology called the Competitive Exclusion Principle, which says that competition between multiple species for a single role will ALWAYS lead to one species winning and the others going extinct or evolving for different roles/niches. We will discuss this more when we run the demos.
The diagram above gives a simple illustration of the Principle.
And that’s all for the mathematical explanations of this part. Even though these explanations were shorter than previous parts, I probably spent 10x longer actually coding the prototype for this part, because of the complexity of the newly introduced interactions.
Demo with 2 Equal Species
Without further ado, let’s see how the introduction of new species changes the simulation! We currently have two species, Modelus Specius and Propagatus Maxima, and they have the exact same stats in all respects. Let’s see the starting conditions:
Running a demo of the two species produces the exact outcome we would expect, they perfectly match each other in population size the entire simulation, stabilizing at 446 members each. It’s not even necessary to show the graph for this demo, but at least we know the code is working as intended so far.
Demo with 2 Unique Species
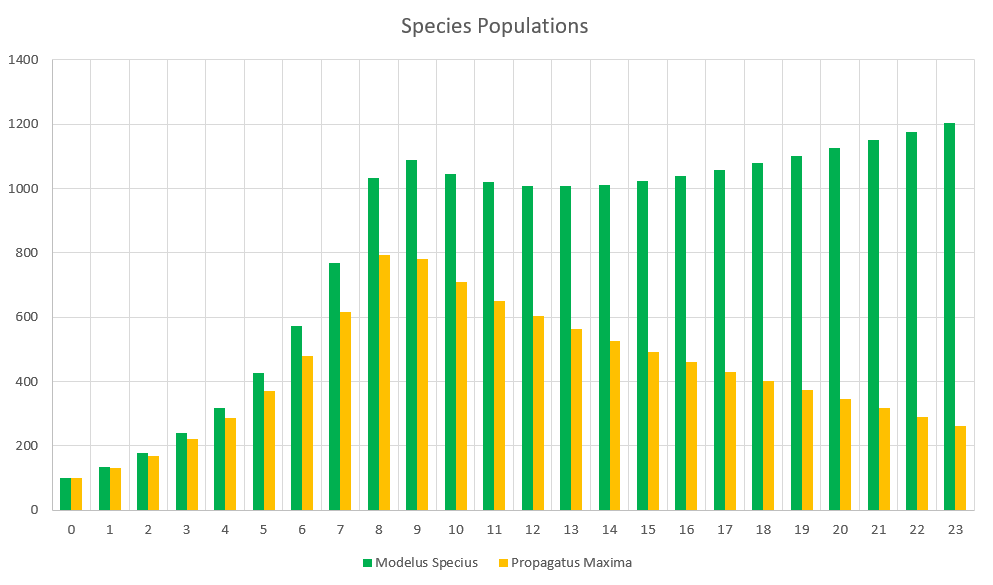
Now for the one we were waiting for, where we assign different stats to each species. We’ll start by doing a very, very small change. We’ll simply increase the strength of Modelus Specius’ muscles from 2.5 N/m^2 to 3.5 N/m^2. A harmless evolution, right?
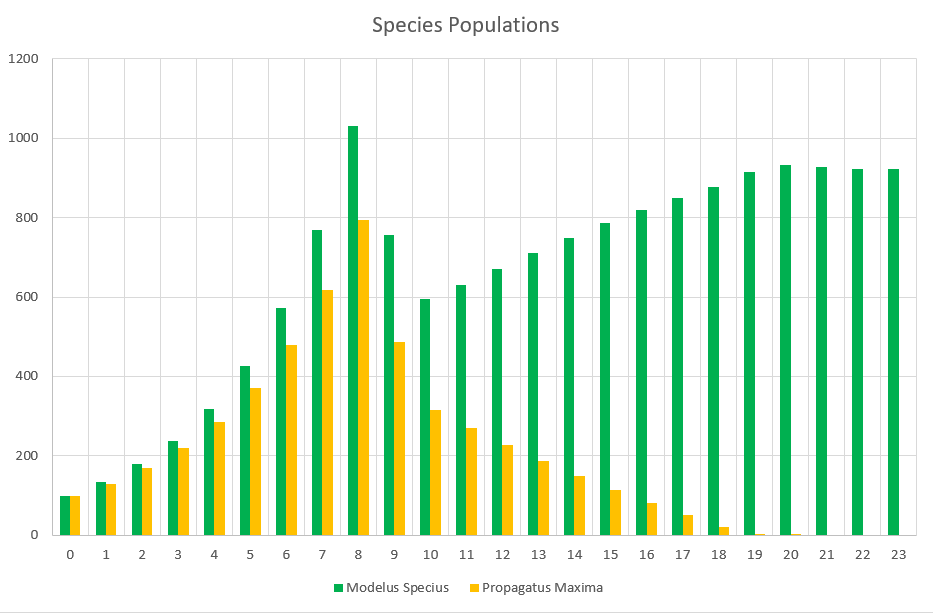
Propagatus Maxima went extinct in 21 months, while Modelus Specius survived and thrived and stabilized at 923 members.
So what’s the story. We can see the exponential growth at the beginning as there is an abundance of food. Notice that Modelus always seems to grow a little faster than Propagatus. Then the food shortage kicks in on the 8th month, and both populations lose a lot of members. However, Propagatus never recovers! Why is this? It’s because when there is an abundance of food competition increases the time spent to hunt but everyone gets all the food they need eventually (unless it takes them sooo long that they run out of time in the month). However, after the shortage starts, there is only so much food to go around every month. Modelus’ slight speed advantage lets them win more of the scarce food on month 9, which leads to a bigger gap between the two species’ populations by month 10. This bigger gap allows Modelus to win even more of the food, and the cycle continues until Propagatus goes extinct. What does this remind you of? That’s right, the Competitive Exclusion Principle. This is a perfect example of the principle in action, since both species are hunting the same “Food” which makes them competitors for the same niche.
A niche is akin to a “role” of a species in an ecosystem, defined by where it lives, what it hunts, and other such factors.
Interesting to note that even such a small competitive advantage of Modelus Specius over Propagatus Maxima builds up to a huge difference in population, and will eventually lead to Propagatus going extinct. This is exactly what is described by the Competitive Exclusion Principle, and it’s fascinating that this pattern emerged without us even specifically trying to put it into the algorithm. We simply modelled realistic interactions and have started to produce a realistic system! I have high hopes for where this algorithm can go!
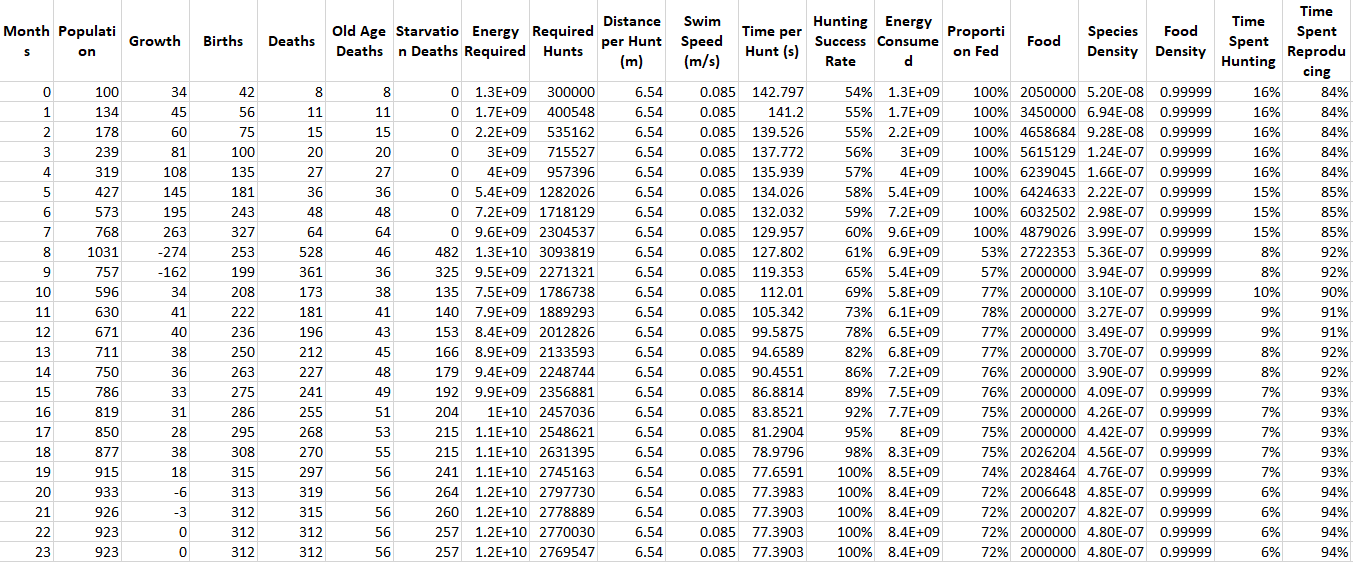
Just a quick aside, now that we’ve got multiple species I’ll probably skip showing the tables with the monthly statistics since it would just be way too much information (since it’s one table for every species). I can keep posting them though if you guys really want them. For now though, I’ll show you Modelus’ report just so that we can understand what is happening:
What are some of the interesting patterns you see? Well for one thing you can see that the time per hunt goes down every month, and this is because Modelus is facing less and less competition as Propagatus dies off. This gradually leads to them having more free time to reproduce, which increases their birth rate and helps them reach a higher population.
One thing this demo has taught me though is that I feel that the starvation penalties may be a bit too harsh.
Less Severe Starvation Rules
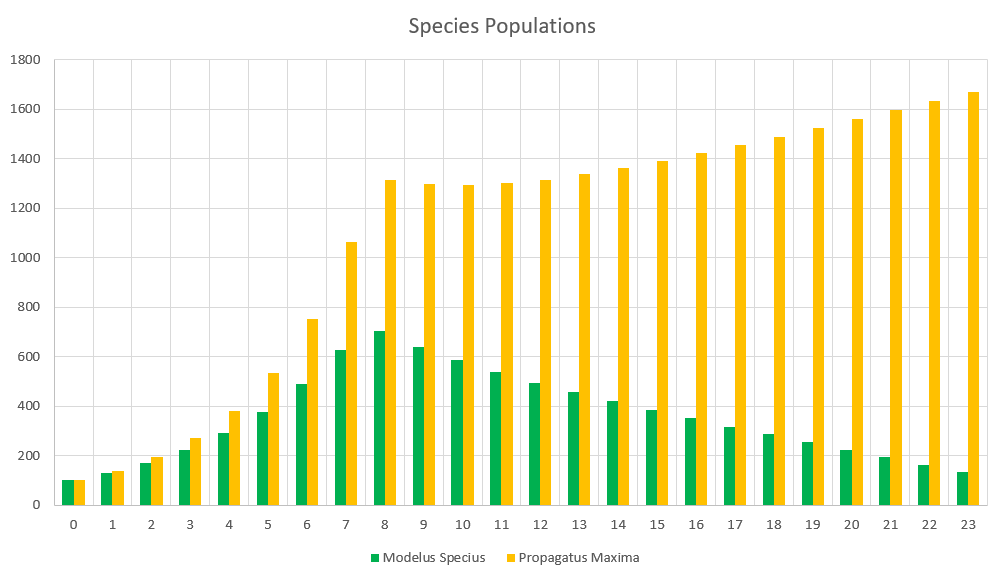
At the moment, 100% of the starving population of a species will die next month. This leads to very sudden extinctions when food runs out. I know that making this value any less than 100% seems very unrealistic since it seems like you’re saying species members can survive over a month without eating. To counter that, I’d say that this percentage can also represent how much energy ALL species members are receiving. 75% Proportion Fed could also mean that ALL species members only receive 75% of the energy they need. So to create a bit of a “softer landing” for species that run low on food, and not letting them go extinct extremely quickly, let’s try making it so that only 50% of starving species members will die. This means starvation is of course still bad but not the game-ending event it was before. This means that your species could technically eat 0 food for an entire month, and only 50% of them would die. Is that entirely realistic? I’m not sure, but we cannot make any more granular changes unless we make the timesteps smaller, and perhaps this is better for balance. Let’s see how this affects the simulation with the same conditions as before.
There we go, a much less severe drop for Propagatus. Even though he looks like he is still destined to go extinct under the current conditions, he at least won’t do so in under 2 years. We can play with the severity of starvation to get the results we like, so I’ll leave that open as a discussion question.
How severe should starvation be?
One more demo with 2 species. This time let’s make Propagatus Maxima into the species he was intended to be. Modelus Specius’ strength will be set back down to 2.5, but instead Propagatus will have 20% higher mating frequency than Modelus.
Holy cow. Clearly increasing mating frequency appears to still be very overpowered. We can revisit potentially balancing that in a future part.
This has been a lengthy post, but luckily with lots of cool new content! We are finally starting to see a lot more of the typical patterns we associate with evolution emerge in the system. I will do a sub-part soon where I’ll crank up the number of species in the simulation to 4, giving each of them unique advantages, and we’ll see who wins the game of evolution! Then after that, we’ll proceed with the next part of the series. Until then, please leave your feedback below!
Summary
New Performance Stats
Competitiveness
Pooled Competitiveness
New Traits
None
Topics for Discussion
- How do I model intra-specific competition (competition within a species)?
- Is it possible to make the time-steps smaller? This would allow for more realistic hunger/starvation modelling. Except this could also make the algorithm very computationally intensive.
- How severe should the consequences of starvation be? 100% death rate of all starving members?