Part 2: Food
The ultimate and eternal goal of life might be reproduction, but the means to that is acquiring food. I can’t blame them, without it, you’re dead.
I know that the last part was very lengthy, so this one will be pretty brief. Recall the list of assumptions in the previous part. One thing I like to imagine as we work on this algorithm is the idea of cutting down that list of assumptions like peeling the layers of an onion. Every assumption we peel off takes us one step closer to the final, realistic algorithm, or the center of the onion. But we have to be careful and do it properly if we don’t want to break down into tears.
Remember in the demo from the last part that the population grew exponentially forever? In this part, we’ll start to address that by introducing the main limiter of life: Food.
From our current list of assumptions, here is the assumption we will address this part:
- Modelus Specius is a flat, tiny, simple, jelly-like organism that lives at the bottom of the ocean.
-
The species is always fully satiated with food and water (Nutrition)
- Which we will replace with:
- Members of the species can instantly perceive food regardless of distance (Perception)
- Members of the species can instantly teleport to perceived food (Movement)
- Members of the species can completely consume the food and gain 100% of the energy. (Hunting/Metabolism)
- The species is equally distributed/dispersed across the world (Demographics)
- The planet is one giant ocean of equal pressure water that is equally accessible to the player (Geography/Terrain)
- Members can reproduce as many times as they want, instantly, with no pregnancy/gestation period. (Reproduction)
- The species reproduces via asexual reproduction, spawning fully developed offspring that can themselves immediately begin reproducing. (Mating)
- The species does not change in physiology as they age (Aging/Ontogeny)
- The species is fully aquatic (Terrestriality)
- Members of the species are solitary and do not cooperate with other species members in any way. (Cooperation/Sociality)
- The species has no parental instincts, and will immediately abandon offspring (Parenting)
- The species is perfectly adapted to its environment and suffers no death or disease from environmental conditions (Environment)
Calories
The basic unit of measuring food and consumption will be the calorie (specifically the food calorie or kilocalorie). It can be used to measure the energy yielded from food and the energy needed by organisms to survive and do things. Every month, the species will have a total number of calories they need to eat. If they fall short of that number, then they lose some members to starvation. First let’s calculate the calories needed by the species.
Every species member will have a Base Metabolism, which refers to the standard amount of calories they will burn on a typical day just by existing. This is equivalent to a concept called Basal Metabolic Rate in biology, but is not exactly the same since our scenario is still so simplistic. Also, since our organisms are so simple, their base metabolism will not fluctuate day by day, since whereas in real life activities like hunting, hibernating, or reproducing can drastically change the amount of calories you burn.
Modelus Specius is a very small and simple organism, so we will give him a base metabolism of 10 calories per day, which comes out to 300 calories per month. Then we multiply this by the total population at a given timestep, and that gives us the total number of calories needed by the species at a timestep.
Calories Required = Base Metabolism * Population
Starvation
Since we are using averages, let’s say that the ratio of calories consumed to the calories required represents the proportion of the overall population that is fed (Proportion Fed). The species only eats as much as they require and no more, so Proportion Fed is capped at 1.00.
Say the species only consumes 75% of the calories they need. This makes the Proportion Fed 0.75. This could mean that 75% of the population receives all the calories they need and suffer no health consequences, and 25% receive no calories and die of starvation. However, this could also mean that 100% of the population only receives 75% of the calories they need, and as a result of the health consequences (aka diseases) they get from this, 25% of the population dies. So, in a way, these deaths are theoretically from starvation AND starvation-induced disease. The statistic could also represent any range of possibilities in between.
Let’s show how this would be represented mathematically:
Proportion Fed = Calories Consumed / Calories Required
Deaths from Starvation = Population * (1.00 – Proportion Fed)
Updating the Algorithm
Recall the current equations:
Deaths = Initial Population * 1 / Lifespan
Intermediary Population = Initial Population - Deaths
Births = Intermediary Population * Available Reproducers * Mating Frequency * Litter Size
Population = Intermediary Population + Births
Now we’ll add in deaths from starvation. Remember, the order of calculation is very important, so this is the order we will follow:
- We start with the current population of the species
- Next, all of the old species members die of old age
- Next, all of the younger species members feed, and those who don’t die of starvation
- Finally, all of the surviving species members reproduce
This is how that looks like:
Old Age Deaths = Initial Population * 1 / Lifespan
Intermediary Population 1 = Initial Population - Old Age Deaths
Proportion Fed = Calories Consumed / Calories Required
Deaths from Starvation = Population * (1.00 – Proportion Fed)
Intermediary Population 2 = Intermediary Population 1 - Starvation Deaths
Births = Intermediary Population 2 * Available Reproducers * Mating Frequency * Litter Size
Population = Intermediary Population + Births
And let’s visualize this with a Life Cycle Diagram:
Straightforward enough. There is one last thing we need to implement though, and that is where the calories come from. There are 3 different scenarios we can have.
Infinite Food
Food can be infinite, in which case we don’t track how much food is being consumed every timestep. We only care about the calories it provides the species. This essentially produces the exponential growth we saw in Part 1 since there is nothing to limit growth. This won’t be the approach we take.
Finite Non-Renewable Food
Food can be a limited/finite source. Eventually the calories will run out and the species will go extinct through starvation. This is also not the approach we will take, since it means the species will go extinct very quickly.
Finite Renewable Food
Finally, we can have food be a limited but renewing source. THIS is the approach we will go with, since it best simulates an ecosystem until we can start later adding in details like autotrophy and predation.
At this point, imagine the food to be individual little clouds of glucose floating in the water. We’ll say that each one yields 10 calories when consumed, and that the environment begins with 50,000 of them at the start of the simulation. Now let’s model this in the algorithm:
First, we calculate the total calories available from the food.
Calories Available = Food Amount * Calories per Food
Calories Required = Base Metabolism * Population
Calories Consumed = Calories Required OR Calories Available #Whichever is smaller
Food Consumed = Calories Consumed / Calories per Food
Food = Initial Food - Food Consumed + Food Generated
Proportion Fed = Calories Consumed / Calories Required
...
And from this point on we’ve got the equations you saw above.
Calories Consumed will be capped by the total amount of calories available in the environment. Also, as the calories are consumed the amount of food is reduced. The food is also replenished at a steady rate every month (Food Generated).
Demo
With all of the equations finished, let’s plug into the demo and see the outcome.
Starting Conditions
- Simulation Time = 24 months
- Modelus Specius
- Starting Population = 100
- Available Reproducers = 1.0
- Mating Frequency = 1/month
- Litter Size = 1
- Lifespan = 3 months
- Base Metabolism = 300 calories/month
- Food
- Starting Amount = 50000
- Calorie Yield = 10 calories
- Regeneration Rate = 50000/month
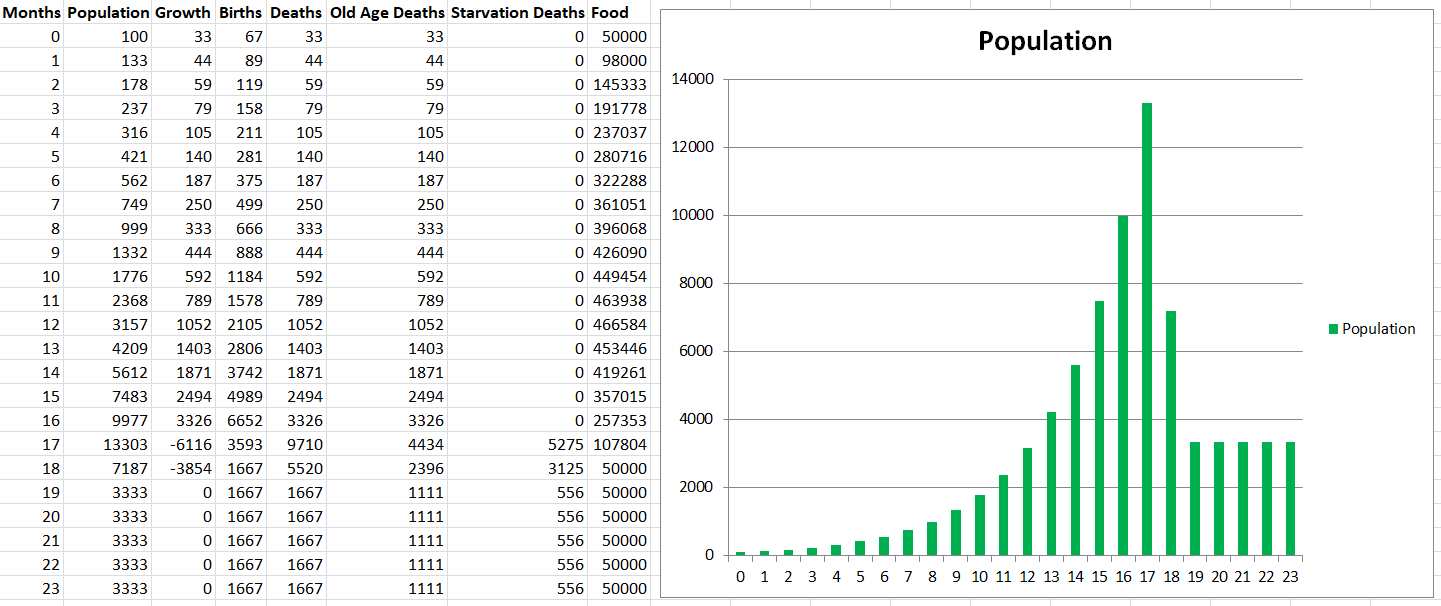
There we go! Now the population is limited by the amount of food that is available in the environment. Notice that at first there is so much food available that Modelus Specius essentially grows exponentially. However, once the surplus runs out, famine hits and starvation rates cause the population to fall and stabilize at a much lower level. Interestingly, this is the furthest that most mathematical modelling of populations goes (except they sort of incorporate food with habitat space and other factors into an overall “carrying capacity” resource). So, from this point on, we are venturing into uncharted territories with the algorithm. It’s exciting to see how things develop!
This current model for food does assume many things to make it simple, and we will expand on these in the future to make the algorithm more realistic. These include:
- Food is equally distributed between all species members with no competition
- All the required food could be eaten on the last possible day of the month and still meet the monthly quota, instead of having to be eaten at regular intervals
- No discrimination between food groups for calorie intake
- There is no such thing as storing food either physically or through fat reserves
Summary
New Performance Statistics
Calories Required
Calories Consumed
Proportion Fed / Starvation Rate
Starvation Deaths
New Traits
Base Metabolism
Topics for Discussion
Suggestions and feedback are welcome!