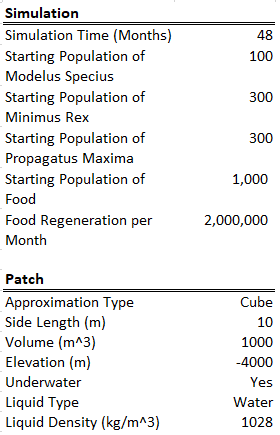
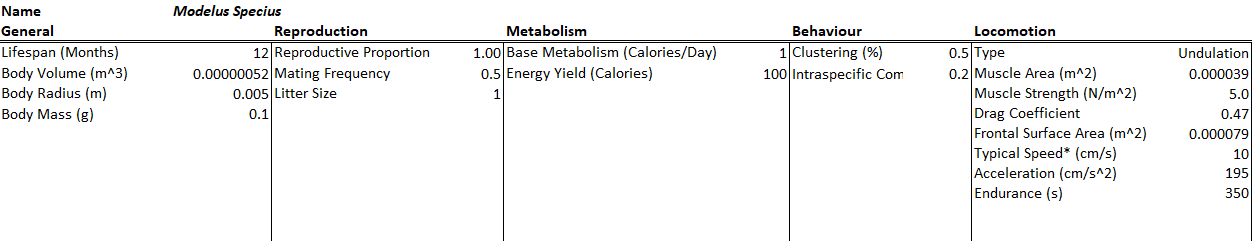Part 7: Predation
At the moment, all of the species hunt for the same free-floating clouds of glucose that we’ve been calling “Food”.
Boring!
Now that we have multiple species let’s add the first step to realistic feeding, carnivores!
Now that we’ve added other species to the mix, and gotten the nitty gritty of competition out of the way, we can start to make this model a lot more interesting. These next few parts will have a lot of juicy content, but will also involve some difficult conceptual hurdles, so it’ll be interesting to see how we make it past them. In fact, my notes for the parts after these next few posts are sparse, because it will depend so much on what we come up with for these next few parts.
Predation is a VERY complex topic, so we will be breaking it down into several parts. Today we will tackle the basic concept of catching and feeding on other species, and how that changes the population dynamics of the ecosystem (as well as how their speeds, accelerations, and endurances are pitted against each other). In future parts, we’ll address Combat, Parasitism, Scavenging, Prey Selection, Heterotrophy vs Autotrophy, and Cannibalism. By the end of implementing all the features related to predation, we’ll have a MUCH more robust algorithm on our hands. We’ll also see that the Starvation Deaths performance statistic is actually a very complex stat derived from many, many, many interplaying factors. It will be the stat that likely fluctuates the most between months, and it makes sense because success in hunting is a large part of survival. Many evolutions of species will simply be to improve success in hunting and reduce Starvation Deaths.
Let’s break down the following assumption from our list of assumptions:
- Modelus Specius is a flat, tiny, simple, jelly-like organism that lives at the bottom of the ocean.
- Members of the species can completely consume the food and gain 100% of the energy. (Hunting/Metabolism)
- Members of the species can instantly perceive food regardless of distance (Perception)
- Members can reproduce as many times as they want, instantly, with no pregnancy/gestation period. (Reproduction)
- The species reproduces via asexual reproduction, spawning fully developed offspring that can themselves immediately begin reproducing. (Mating)
- The species does not change in physiology as they age (Aging/Ontogeny)
- The species is fully aquatic (Terrestriality)
- Members of the species are solitary and do not cooperate with other species members in any way. (Cooperation/Sociality)
- The species has no parental instincts, and will immediately abandon offspring (Parenting)
- The species is perfectly adapted to its environment and suffers no death or disease from environmental conditions (Environment)
We will instead replace it with:
- Modelus Specius is a flat, tiny, simple, jelly-like organism that lives at the bottom of the ocean.
- Members of the species will always win combats against smaller individuals, and lose to larger ones (Combat)
- Members of the species always consume 100% of the energy of defeated prey (Metabolism)
- Members of the species can instantly perceive food regardless of distance (Perception)
- Members can reproduce as many times as they want, instantly, with no pregnancy/gestation period. (Reproduction)
- The species reproduces via asexual reproduction, spawning fully developed offspring that can themselves immediately begin reproducing. (Mating)
- The species does not change in physiology as they age (Aging/Ontogeny)
- The species is fully aquatic (Terrestriality)
- Members of the species are solitary and do not cooperate with other species members in any way. (Cooperation/Sociality)
- The species has no parental instincts, and will immediately abandon offspring (Parenting)
- The species is perfectly adapted to its environment and suffers no death or disease from environmental conditions (Environment)
Changes to the Algorithm
This part again included some major changes to the code, so I had to do another major overhaul to make things cleaner and more organized. I also had to reorder how some things were calculated to make it easier to implement predation and the upcoming features. Here is a summary of the changes:
- Prey lists and predator lists. Every species now has a list of species it preys on and a list of species that are predators to it. Instead of just calculating hunting statistics once for every species, we now calculate different statistics for each prey that they hunt. These include Required Hunts, Available Hunts, Time per Hunts, etc. The differences between how the predator favours the prey is based off of the priority that predator has for hunting each prey. If a species has a total energy requirement of 1000 joules for their entire species, and they have a prey priority of 50% for Species X, then they will try to get 500 joules of energy through hunting Species X (however many hunts that would be). At the moment, all species have only 1 prey, the food clouds, with a priority of 100%, so this makes no change to the simulation’s outcome. However things will change over the course of this part as we make species prey on each other.
- Body mass, acceleration, and endurance added as traits. I will explain why below.
How Do we Implement Predation?
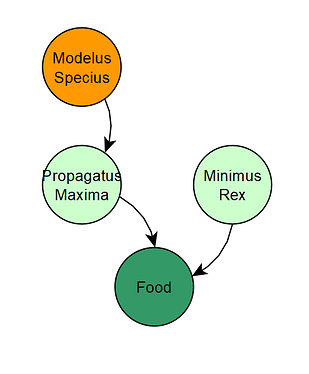
As a result of implementing predation, Modelus Specius will now be a carnivore. Carnivores will instead consume members of other species instead of the clouds of glucose. In this case, Modelus Specius will feed on Propagatus Maxima, and nothing else. Propagatus Maxima and Minimus Rex will continue to feed on glucose only. We’ll cover herbivores and omnivores in a future part. This gives us the chance to create our first food web!
We can see that it’s pretty simple so far, with Modelus Specius at the top of the food chain and only two species below him.
The major changes to the simulation by adding predation will be:
- Hunting prey that can move and escape you. So we need to come up with an equation that determines how successfully predators can catch prey.
- Hunting prey whose population can grow or shrink dynamically. This will not need to be specifically coded because it will naturally result from the changes we make. However, it will be interesting to observe how it changes the results of the simulation.
Planning how to start tackling this issue can be a pretty tricky concept, so let’s break it down into its constituent elements and think about it logically.
A predator can either be in two situations with the prey.
- The predator is faster than the prey.
- The predator is slower than the prey.
New Traits
Before we consider these two scenarios, I added 3 new traits to the mix to help in the calculations that you will see soon.
Acceleration is a trait representing a species’ initial acceleration going from not moving to his max speed. It is calculated by the simple physical equation of Acceleration = Force / Mass. Remember that force in this case is the force of the muscles, which we already have traits for. The units of acceleration are in meters per second squared.
Body Mass is a trait representing the mass of the species. So far, it is only used in calculating the acceleration of the species. The units of body mass are in kilograms.
Endurance is a trait representing how long the species can go at its max speed before it tires and has to stop. The units of endurance are in seconds.
Faster Predator
If the predator is faster, then it’s quite simple. The predator can overtake the prey in speed and catch him. In this case, we can refer to the predator as a “Speed Hunter”, since he’s using his greater speed to catch the prey in their chases.
There’s only one caveat. What if the predator starts 100m away and gets tired after just a couple meters of running? Even if he’s faster than the prey, it’s irrelevant because he started so far away he couldn’t traverse the distance. Thus we can see that even if the predator is faster than the prey, he has to have the endurance to overcome the distance between them. So a more accurate statement would be:
“If the predator is faster than the prey, AND the time it takes to catch the prey is less than or equal to the predator’s endurance, the predator will always win the chase.”
Mathematically, we’ll represent this using a fraction. We’ll divide the endurance of the predator by the average time per hunt. We’ll cap the success rate of the predator at 100%. This gives us the following equations:
IF Predator Speed > Prey Speed
THEN Success Rate = Endurance / Time per Hunt
NOTE: For or any astute readers, you may recall that Time per Hunt is a performance stat that is affected by inter and intra specific competition! More competition increases the time per hunt. This means that increased competition makes it less likely that a predator will have enough endurance for all their hunts, since sometimes they’ll spend time chasing a prey that gets caught by someone else and wastes some of their endurance.
Also, remember that we added in a new trait called acceleration! Actually calculating a detailed realistic way of implementing varying speeds and accelerations into the hunting equation would be a nightmare. So the simpler way that I will tie in acceleration is by comparing the acceleration of the predator to the acceleration of the prey. If the predator has a higher acceleration than the prey, this gives him a bonus to his speed. If he has lower acceleration, this gives him a malus. This is to represent organisms who are very quick at accelerating and reaching their top speed and catching their prey (or getting away from their predators). So we’ll update the equations to this:
IF Predator Speed * (Predator Acceleration / Prey Acceleration) > Prey Speed
THEN Success Rate = Endurance / Time per Hunt
However, what if the predator does NOT have the endurance to outweigh the average time per hunt? Notice that the relationship is a simple ratio, so if the endurance is half of the average time per hunt, then that means the predator will win half of the chases. This represents that half of the time, the predator is close enough to catch the prey. The other half of the time, he starts so far away that he gets tired before he catches up to the prey (even though he is faster).
This seems like a good equation for now. If we find that it favours the predators or the prey too much, we can come back and rebalance it. Let’s see a quick visual demo of what we discussed:
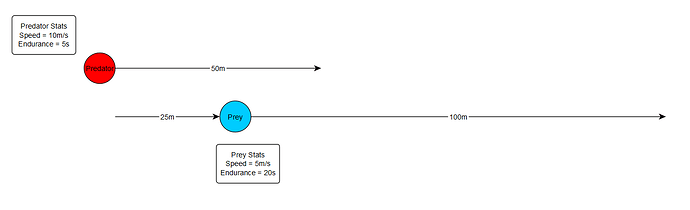
Let’s say that the prey starts 25m away, and both species have equal acceleration so there is no bonus/malus to the predator. We can see that the time it will take the predator to catch the prey is just the distance he starts away from the prey, divided by the difference in their speeds:
Time per Hunt = Average Distance of Predator from Prey / (Predator Speed - Prey Speed)
Time per Hunt = 25m / (10m/s - 5m/s)
Time per Hunt = 25m / 5m/s
Time per Hunt = 5s
Notice how the prey has a much higher endurance than the predator. But it doesn’t matter! Since the predator is faster, he catches up to the prey in 5 seconds, exactly his endurance limit. Using the equation we have above, that gives the predator a success rate of:
Success Rate = Endurance / Time per Hunt = 5s / 5s = 1.0 = 100%
The average hunt is exactly within the endurance limit of the predator, so he catches the prey essentially an average of 100% of the times that he chases him.
Slower Predator
Ok, but what if the predator is not faster than the prey? In that case, there’s only one possible scenario where the predator could still win. This is what we’ll call an “Endurance Hunter”.
Imagine a predator starts to chase a prey 10 meters away. The prey has a speed of 10 m/s, but only 1 second of endurance. Meanwhile, the predator has a speed of 1 m/s but has 100 seconds of endurance. The prey outruns the predator for the first second, but then tires. Meanwhile, the predator second by second gets closer, until eventually catching the prey on the 20th second.
So even if the predator has a lower speed than the prey, he can still win if the overall distance he traverses is greater than the distance the prey traverses PLUS the distance of the gap between them. How does this look mathematically?
First, let’s define the distance traversed during a hunt as the speed of the organism multiplied by the endurance of the organism:
Predator Distance Travelled = Predator Speed * Predator Endurance
Prey Distance Travelled = Prey Speed * Prey Endurance
Now, combining this with what we discussed above we get:
IF Predator Speed * (Predator Acceleration / Prey Acceleration) <= Prey Speed
AND Predator Distance Travelled >= Prey Distance Travelled + Average Distance from Predator to Prey
THEN Success Rate = Predator Distance Travelled / (Prey Distance Travelled + Average Distance from Predator to Prey)
Notice that again we are using a fraction for determining the success rate. This time we compare the distance travelled by the predator to the distance travelled by the prey plus the gap between them. This means that the total distance travelled of the predator would equal the total distance travelled of the prey plus the average gap between them for the predator to have a 100% success rate.
Let’s use another diagram to visualize this scenario:
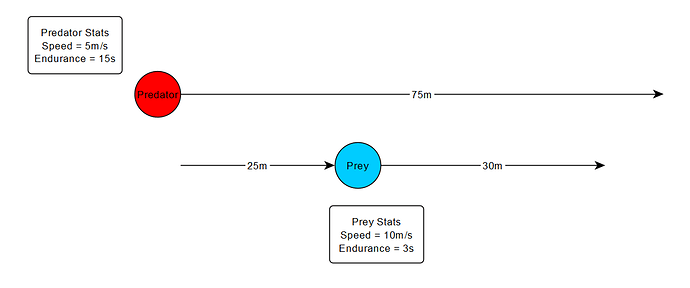
Again the prey starts 25m away from the predator. Although the prey has a higher speed than the predator, he tires quickly while the predator continues chasing due to his high endurance. Eventually the predator catches the prey, at the 55th meter. The time the hunt takes is the total distance the predator has to move to catch the prey, divided by the predator’s speed.
Time per Hunt = (Prey Distance Travelled + Average Distance from Predator to Prey) / Predator Speed
The predator’s average success rate is modelled by:
Success Rate = Predator Distance Travelled / (Prey Distance Travelled + Average Distance from Predator to Prey)
Success Rate = 75m / (30m + 25m) = 75 / 65 = 1.00 = 100% (Capped at 100%)
Notice that you could have an alternate scenario where the predator’s distance travelled is less than the prey distance travelled plus the average distance from predator to prey. In this case, the success rate would just be the ratio of the predator’s distance travelled to the denominator.
Assumptions
Now what are some of the assumptions that this model is making? Well it assumes that predators and prey always have their maximum endurance available when chasing. What if a predator starts a chase with only half endurance? Or a prey with only 20% endurance? In this case it might make it better to see endurance as the AVERAGE endurance of members of that species when a hunt is initiated. We could keep this in mind though and revisit it in a future part (yes I know I sound like a broken record when saying that).
Order of Calculations
A key question to ask ourselves here is, what order do we calculate predation changes? The problem is that predation calculations for one species will affect the overall calculations of other species. Do we calculate the predation of herbivores first, and then the carnivores? Do we randomly pick one species at a time and calculate predation on it and keep rotating until we’ve hit all species?
The solution I’ve gone for here is to calculate it simultaneously to starvation. Is this entirely realistic? Perhaps not, because it’s currently possible that a species is preyed on at the beginning of the month but still contributes towards the overall hunger and thus starvation of the species over the course of the entire month. However, it means we avoid having to worry about who to calculate predation for first which would be a HUGE hassle on its own, so for now I think it’s a worthy sacrifice.
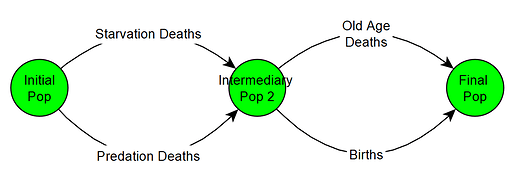
We can visualize the current life cycle of organisms using the following Life Cycle Diagram:
So the way it works is we start with the initial population, and we calculate the food it hunts and the number of individuals that are hunted first. Then the members who die from starvation and predation are killed off. From the survivors, offspring are born, and then some of those survivors also die of old age. The final group of survivors plus the offspring form the population of the next simulation step.
Demo
Now that we’ve ironed out all the additions of predation, let’s run a demo to see how things have changed.
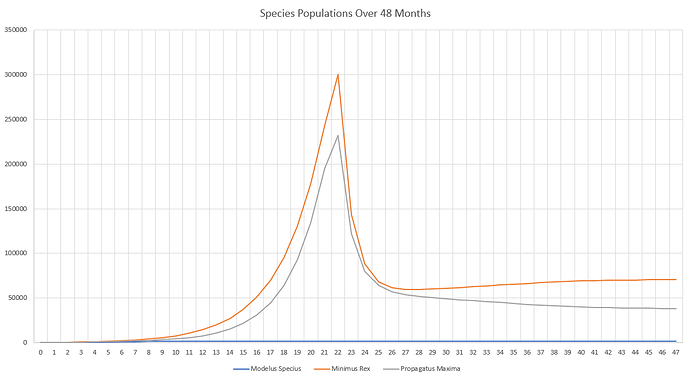
The final populations of the species were:
Modelus Specius - 2,045
Minimus Rex - 70,679
Propagatus Maxima - 38,211
It’s good to see that the simulations have not become chaotic as I was worrying! It seems that the many soft caps we’ve introduced, such as intraspecific competition, interspecific competition, spatial population density, movement speed, and others have helped “cushion” major upheavals from disrupting the population numbers.
From looking at the graph we can see the typical rise in population until we hit the famine on the 22nd month, and then a big hit to the “herbivores” (Minimus and Propagatus). We can also see that once the shortage hits Minimus begins to outperform Minimus at being the dominant glucose-eater.
Meanwhile, although Modelus looks like he’s off the charts, he’s actually maintaining quite a stable population at several thousand members. He was also largely unaffected by the famine, catching essentially just as many prey in the 22nd, 23rd, and following months as he did before.
One thing that I noticed when balancing the simulation was that the predators are very overpowered at the moment. If I make them just even slightly more powerful than the prey in terms of speed or endurance, they will completely eat all the prey and then make themselves starve to extinction. The reasons for this are because perception and combat haven’t been implemented yet. The predators currently know where all prey are at at all times, and always win combats against them. They also suffer no deaths from intra-specific competition, only delays to hunting times. So the predators are extremely and unrealistically efficient. Once we implement these features, predators won’t be as omnipowerful and we’ll start seeing more realistic balances of numbers. Still, it’s cool to see that the predators are naturally forming a smaller proportion of the ecosystem than the prey, and are also reaching stabilized population numbers within 4 years of the simulation.
This part included some major changes, so get ready for some “bugfixing” sub-parts to come up in the next week or so if I run into any bugs or flaws with the implementation from this part. Anyways, it’s really cool to see these features making it into the algorithm and to watch the evolution get slowly and slowly more realistic! Now that we’ve got the basics of predation in place, stay tuned for the content we’ll be able to add next!
Summary
New Performance Statistics
Caught Hunts
Predation Deaths
New Traits
Acceleration
Body Mass
Endurance
Topics for Discussion
- Comments and feedback are welcome!