Refactoring movement is one of the other things I would like changed for the 0.3.3 release. Currently, we only have one movement organelle, flagella, whose speed is only limited by your ATP store, which isn’t very realistic. Adding 10-20 flagella to your cell allows you to be flash—moving faster than the game can process, resulting in a crash—and doubling your flagella amount doubles your speed. There should be a logarithmic (if not hyperbolic) taper, which can be solved by factoring in drag.
The basic, simplified formula for drag that we will use is R = ½ρCAv². ρ is the density (which in our case will be a random constant that we will chose to make the simulation look good), C is drag coefficient (which is basically the shape of the front half of the object, more on finding this later), A is the cross-sectional area (which is the longest line of hexes perpendicular to the microbe direction), and v is the velocity of the object. The velocity is a number that we will be getting from the physics engine, which uses F = ma and vₒ = vf + a∆t (where the mass is the number of hexes and the force is number of flagella multiplied by a constant).
We know everything except for C, which can be found using this nifty table:
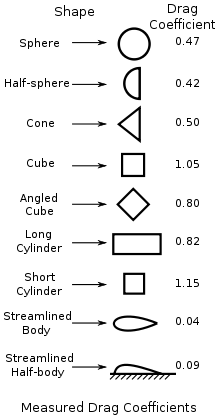
After you exit the editor, an algorithm will attempt to figure out to which of the above shapes the cell is closer to, and will approximate the drift coefficient.
To move the microbe we will just do this:
v = 0 // last frame velocity
Every frame do
Find R // The drag force using the predefined constants ρ, C, and A, and the last fram velocity
Find F // Add all of the forces generated by flagella (constant flagella force multiplied by cosθ)
Find I = (F - R)*dt // The impulse
physicsComponent.applyCentralImpulse(I)
v = physicsComponent.getVelocity() // Get the new velocity
end
I am kind of tired now, so I’ll get to cilia later, but in short, cilia have a much smaller thrust force, but a larger torque. This torque will be affected not by pressure drag as above, but by frictional drag (which depends on the cell outline). This means that circular and smaller cells turn faster, and larger and weirdly shaped cells turn slower.
To be continued…
Continued:
The above half talked about thrust. This second part will describe rotating your cell. Both flagella and cilia have a thrust component, with the former have a greater thrust and the latter a greater torque. Pseudopods will be somewhere in between, e.g.:
Thrust Torque
Flagella 10 2
Cilia 3 10
Pseudopods 6 4
For fricitonal drag, we will use a slightly less scientific formula. The frictional drag is basically equal to the surface area multiplied by a number (since sluid density, surface material, and velocity are assumed to be constant). We will assume cells are two dimensional and will just use the perimeter instead of surface area (which can easily be found by calculating the number of hex edges on the outside of the cell). We will then multiply this by the “unevenness” of the membrane (which is the perimeter sqaure devided by internal area, or total number of hexes). I am thinking of letting players create star-shaped cells for the next microbes (since a lot of people have been asking for them, and they are realistic by using microtubules), they will just be detrimental because rotating will be much harder.
To reiterate, this is going to be our semi-realistic calculation of frictional drag that will be used as a factor to decrease the torque:
Torque calculated from movement organelles * Area / (perimeter ^ 3) * random constant
And that concludes our brief science lesson. Yay for physically accurate movement and new organelles!