I saw the metaballs concept on my Facebook feed, and figured I should probably makes this post (about 4 years overdue). One of the things I was working on back in 2016 was figuring out a good solution for 2d and 3d organism editing. There are quite a few constraints that a good editor should meet, but the 3 main ones is that it should be easy to use (you don’t need a 2 hour long course to design a creature), it should be sufficiently powerful (any creature you can come up with should be possible to create), and it should produce good results (people who aren’t artistically inclined should be able to make good looking creature without much effort). Metaballs, which is what we’ve been discussing using for this purpose since way before TJWhale designed and I implemented the current membrane code, unfortunately don’t satisfy the last two requirements: They are incredibly frustrating to deal with (have you ever tried creating a sausage-like shape like a tail? practically impossible) and the results always look like blobs.
Anyway, introduction aside, after much research and testing out various solutions, I came to the conclusion that the best solution is what is known as “Convolution Surfaces”. Specifically, a variation known as “SCALe-invariant Integral Surfaces”.
The way they work is you place a few points, specify the radius around that point, and connect the points with segments. The convolution surface will then contain all of the “spheres” you placed within its boundaries with very good looking transitions. Unlike metaballs, the surface will be the specified radius away from each point, which lends itself to very fine-grained and intuitive control. It also doesn’t produce unwanted bulges:

In the above image with 3 points connected by two line segments, metaballs would produce the surface on the left while convolution surfaces would product the one on the right. In fact, adding any number of points on the segments between the outer two would not change the shape of the surface, provided they have the same radius.
And here is an image of an ant created using convolution surfaces with a solid and wireframe representation:
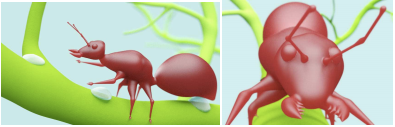
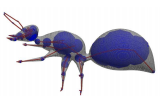
*The above images are taken from the SCALIS paper linked above.
And here’s another example of a hand:

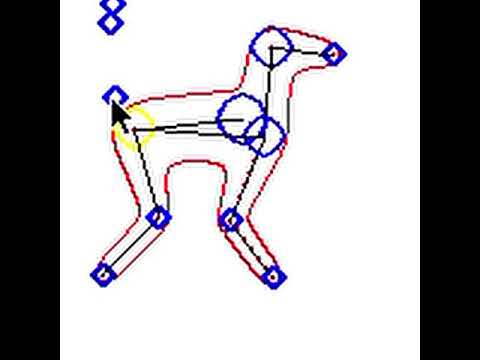
Here’s a prototype that I wrote using convolution surfaces and marching squares for rendering:
It runs at like 2 frames a second because I wrote it in python, is in 2d, and is missing quite a few features (you can see that in some cases the blue circle is outside the red surface, but this is only because I didn’t have time to implement that step), but it is a good demo of what could be.
Another incredibly useful feature is that if you were to put 7 circles in a hexagon grid, it create a near perfect circle, which is something that I tried forever, but was never able to accomplish with the current membrane code:
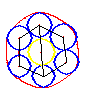
So for the cell stage, using this method we could 1) Have better looking membranes, 2) Have a more deterministic algorithm for membranes, 3) allow concave membranes, and 4) Prevent organelles from spilling outside the membrane. You would just need to have a point in each hex that is part of the cell, and set the “radius” of each point to the bounding sphere of the organelle at that position + some buffer.
For early multicellular, each point could be a cell, and the surface would produce a good looking outline. For organism stage, the points could be organs/muscles. My implementation uses 2 points to define a segments, but the algorithm supports linking 3 (or more) points into a triangle, which produces some interesting results:

The above image is a fin created using triangle primitives.
Feel free to check out my code: GitHub - TheCreator--/SCALIS: Implementation of SCALe-invariant Integral Surfaces
It’s clearly in prototype state, and barely runs (again, python probably wasn’t the best solution for this), but it should give a good starting point to anyone who decides to pick this task up.